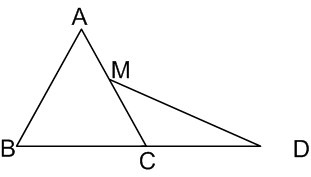
در مثلث متساوی‌الاضلاع ABC به ضلع 2، نقطه C وسط ضلع BD و نقطه M وسط ضلع AC است، مساحت مثلث CMD کدام است؟
1 )
$ \frac{\sqrt{2}}{2} $
2 )
$ \frac{3}{4} $
$ \frac{\sqrt{3}}{2} $
4 )
1
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...