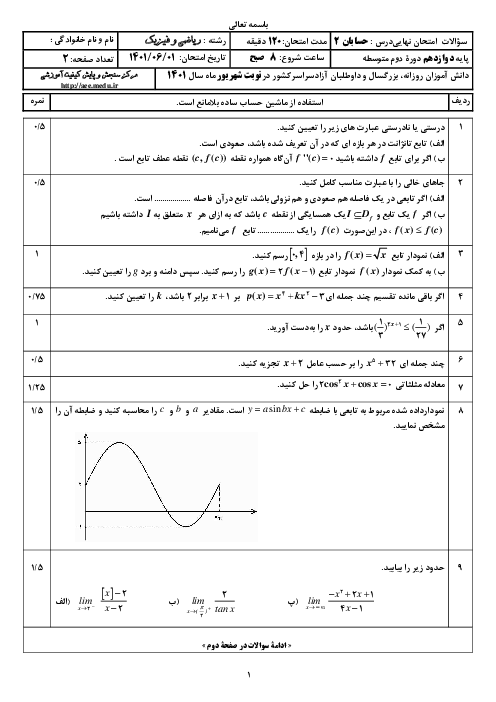
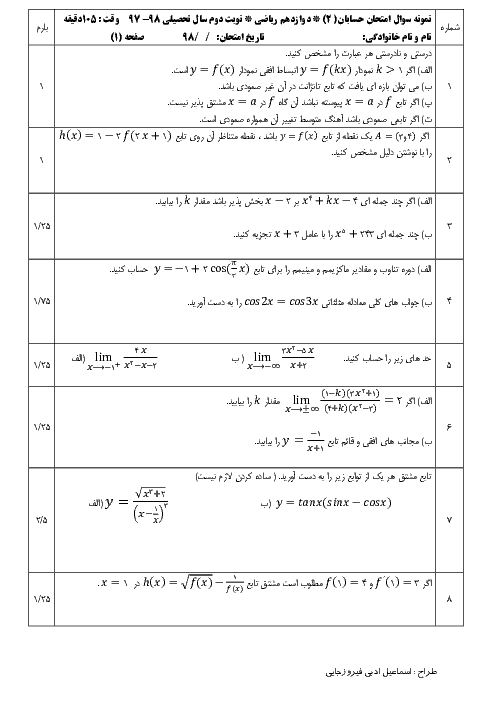
** فصل 3: حدهای نامتناهی- حد در بی‌نهایت
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
نقطهٔ $(-1,-2)$ یکی از محل‌های تلاقی مجانب‌های نمودار تابع $y=\frac{1+a{{x}^{2}}}{1+b{{x}^{2}}}$ است. $a+b$ کدام است؟
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...