نكته: در تابع $f$ مجموعه نقاط شامل نقاطی كه مشتقِ تابع در آن‌ها وجود ندارد و نقاطی كه مشتق در آن‌ها برابر صفر است، را نقاط بحرانی $f$ می‌ناميم.

ابتدا تابع را به‌صورت يك تابع چند ضابطه‌ای می‌نويسيم و سپس مشتق آن را محاسبه می‌كنيم:

$f\left( x \right)={{x}^{2}}\left| x-3 \right|=\left\{ \begin{matrix}    {{x}^{3}}-3{{x}^{2}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\ge 3  \\    -{{x}^{3}}+3{{x}^{2}}\,\,\,\,\,\,\,\,\,\,\,x \lt 3  \\ \end{matrix} \right.\Rightarrow {f}'\left( x \right)=\left\{ \begin{matrix}    3{{x}^{2}}-6x\,\,\,\,\,\,\,\,\,\,x \gt 3  \\    -3{{x}^{2}}+6x\,\,\,\,\,\,\,x \lt 3  \\ \end{matrix} \right.$ 

تابع در نقطۀ $x=3$ مشتق ندارد. حال مشتق تابع را برابر صفر قرار می‌دهيم:

${f}'\left( x \right)=0\Rightarrow \left\{ \begin{matrix}    3{{x}^{2}}-6x=0\xrightarrow{x \gt 3}  \\    -3{{x}^{2}}+6x=0\xrightarrow{x \lt 3}x=0,2  \\ \end{matrix} \right.$

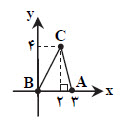
بنابراين مختصات نقاط بحرانی اين تابع به‌صورت $C\left( 2,4 \right),B\left( 0,0 \right),A\left( 3,0 \right)$ است. بنابراين:

${{S}_{\overset{\Delta }{\mathop{ABC}}\,}}=\frac{1}{2}\times 4\times 3=6$