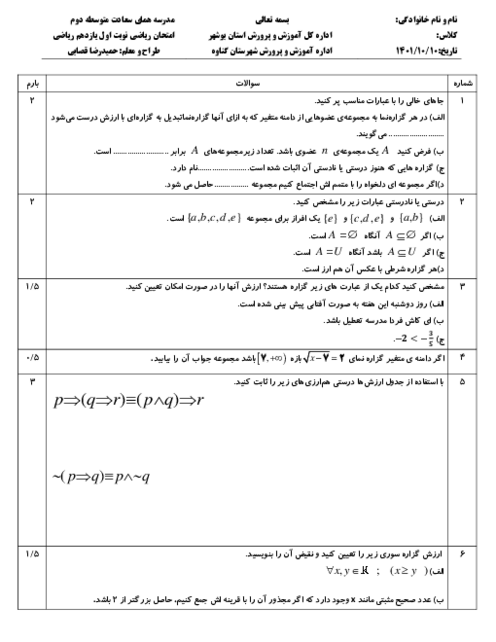
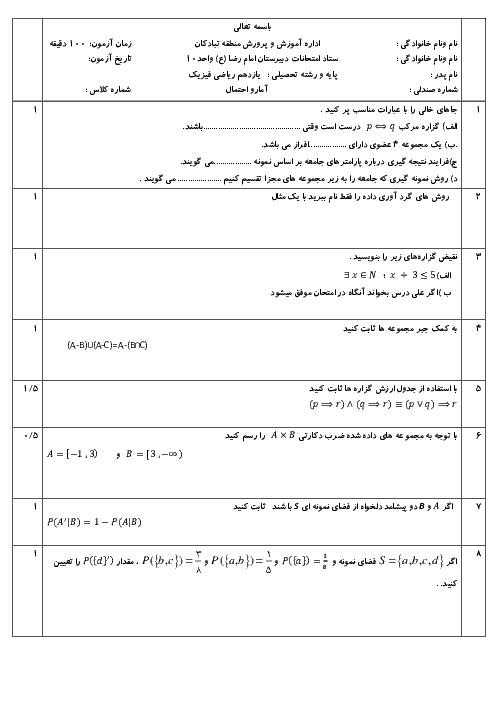
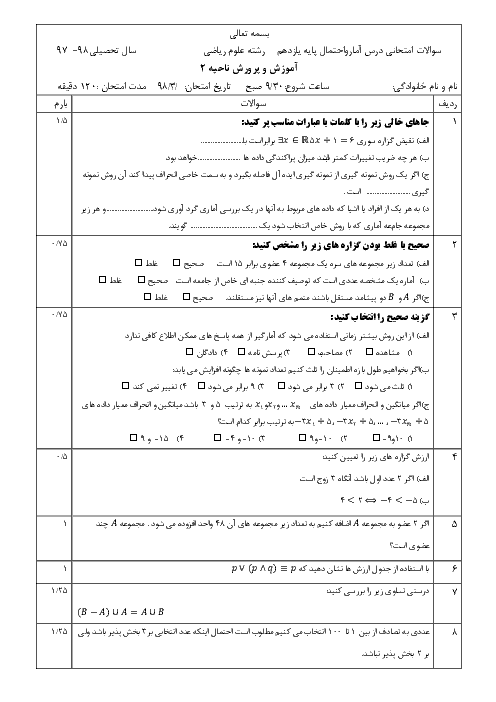
درس 3: قوانین و اعمال بین مجموعه‌ها (جبر مجموعه‌ها)
آمار و احتمال
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
اگر $U=\{1,2,3,4,5\}$ مجموعه‌ی مرجع باشد، آن‌گاه چند مجموعه مانند$A$ وجود دارد به گونه‌ای که $A\bigcup \{1\}=A\bigcap \{1,2\}$ باشد؟
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...