در اثبات نامساوی $\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\ge \frac{4}{\sqrt{x}+\sqrt{y}}$ از طریق اثبات بازگشتی، رابطه‌ی بدیهی به‌دست آمده کدام است؟ ($x$ و $y$ دو عدد حقیقی مثبت هستند.)
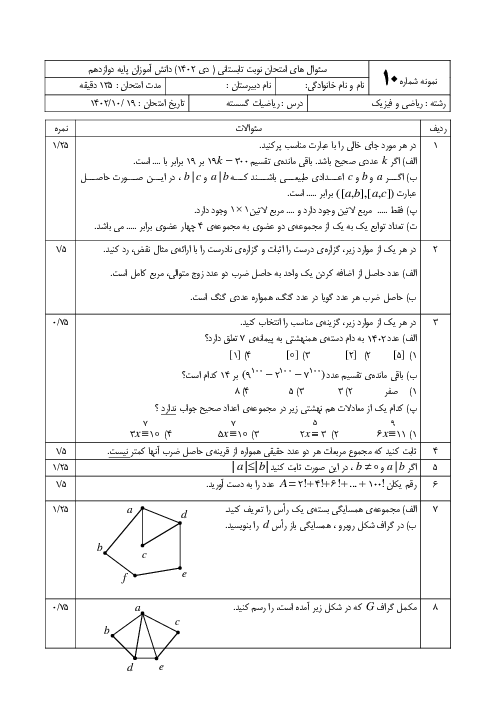
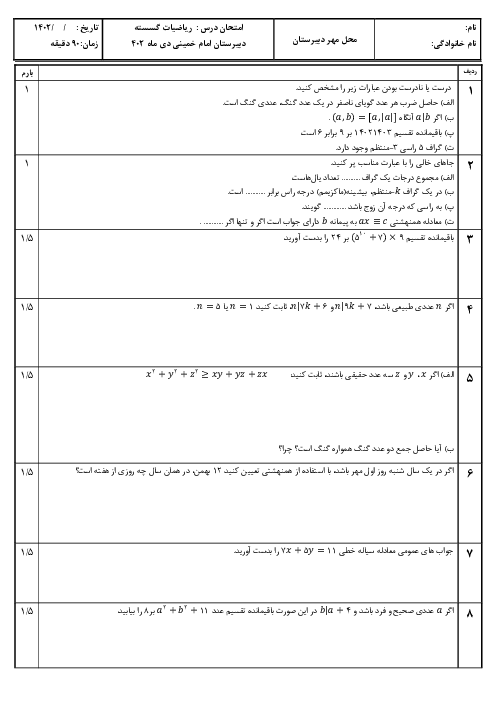
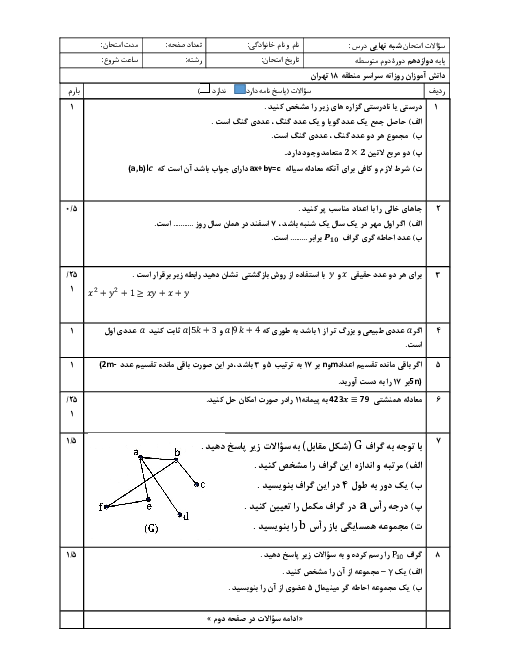
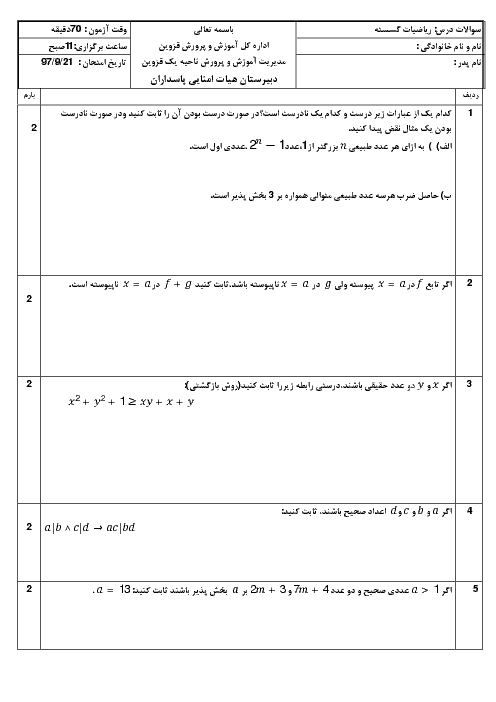
1 )
${{(x+y)}^{2}}\rangle 0$
2 )
${{x}^{2}}+{{y}^{2}}\rangle 0$
${{(\sqrt{x}-\sqrt{y})}^{2}}\ge 0$
4 )
$\sqrt{x}+\sqrt{y}\rangle 0$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...