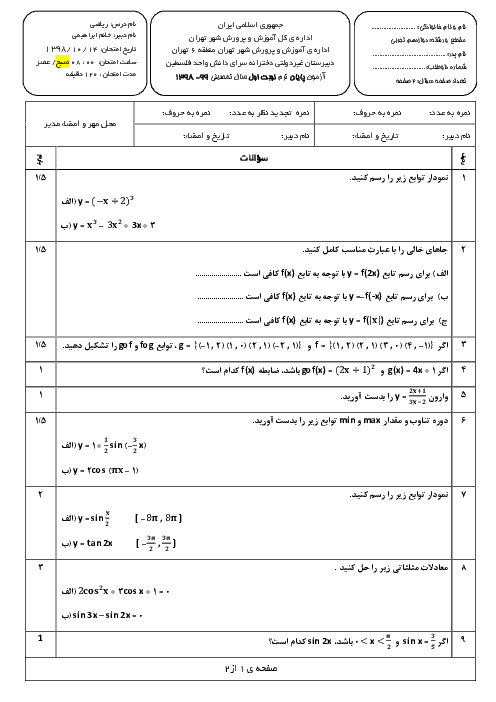
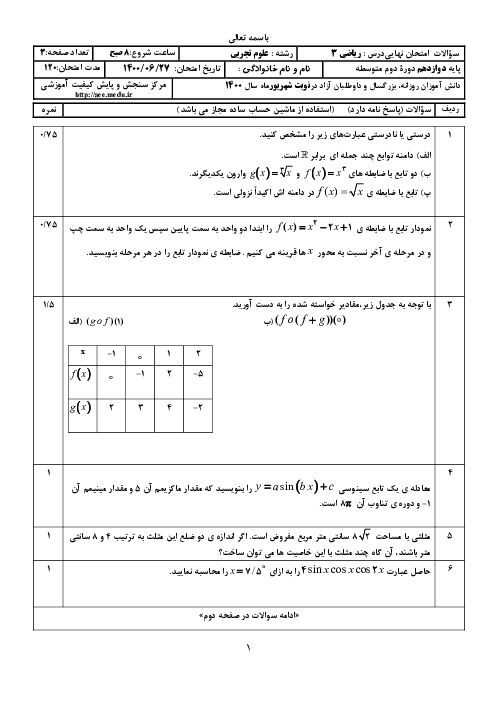
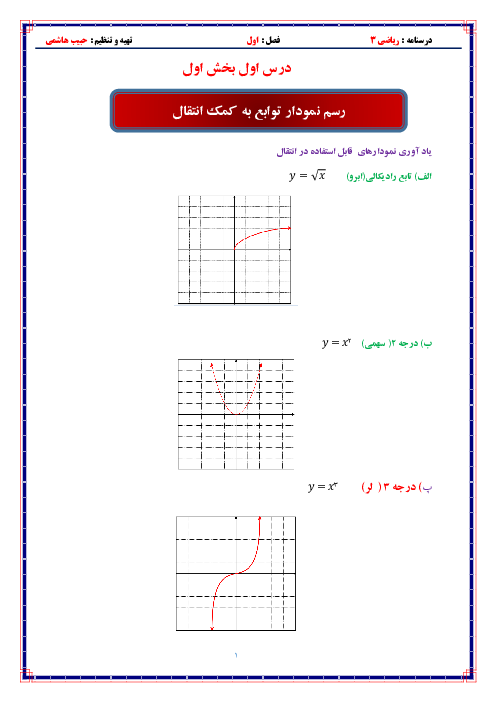
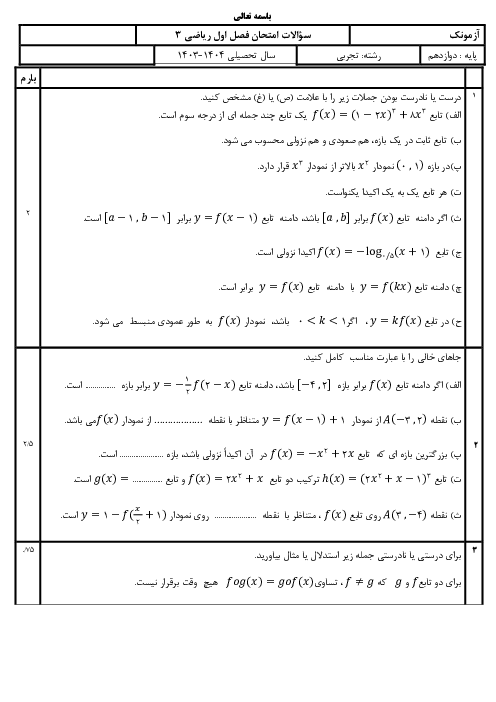
در شکل مقابل نمودار تابع $y=f(x)$ و خط مماس بر آن در نقطهٔ $x=1$ رسم شده است. حاصل $\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)-f(1)}{1-\sqrt{x}}$ کدام است؟
1 )
$-\frac{\sqrt{3}}{3}$
$-\frac{2\sqrt{3}}{3}$
3 )
$\frac{\sqrt{3}}{3}$
4 )
$\frac{2\sqrt{3}}{3}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!