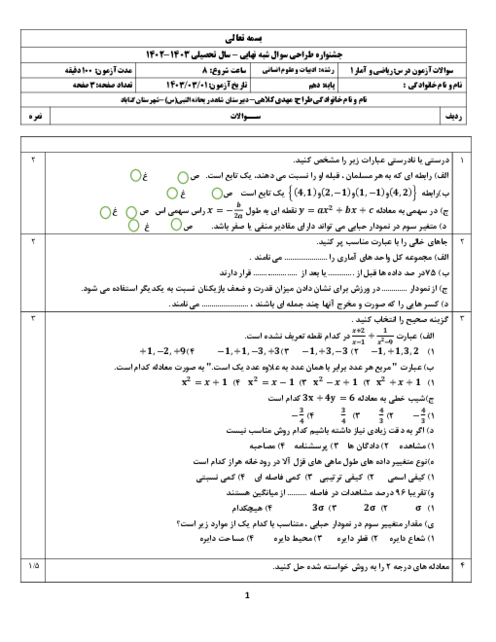
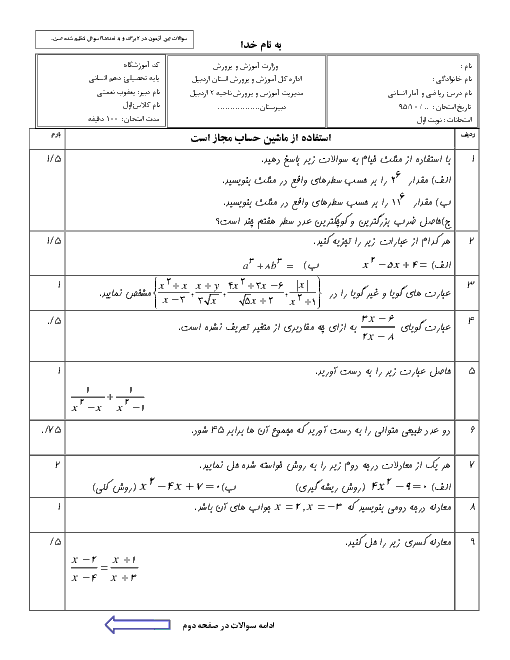
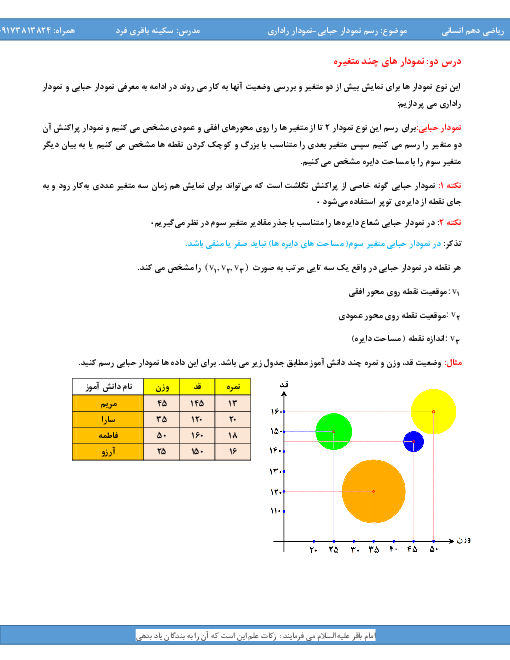
دقت کنید که ریشة معادله در خود معادله صدق می‌کند، لذا ابتدا با جایگذاری $x =  - 2$ در معادله مقدار $k$ را می‌یابیم:

${x^2} + kx + 6 = 0\,\underrightarrow {\,x =  - 2}\,{( - 2)^2} + k \times ( - 2) + 6 = 0$

$ \Rightarrow 4 - 2k + 6 = 0 \Rightarrow 2k = 10 \Rightarrow k = 5$

حال با قرار دادن $k = 5$ در معادله آن را با استفاده از اتحاد یک جملهٔ مشترک تجزیه و حل می‌کنیم:

${x^2} + 5x + 6 = 0 \Rightarrow {x^2} + (2 + 3)x + (2) \times (3) = 0 \Rightarrow (x + 2)(x + 3) = 0$

$\eqalign{
  &  \Rightarrow x + 2 = 0 \Rightarrow x = 2  \cr 
  & x + 3 = 0 \Rightarrow x =  - 3 \cr} $

در نتیجه ریشهٔ دیگ معادله $x =  - 3$ است.

راه دیگر: در معادلهٔ درجهٔ دوم $a{x^2} + bx + c = 0$ در صورت وجود دو ریشهٔ حاصل ضرب ریشه‌ها از رابطهٔ $\frac{c}{a}$ به‌دست می‌آید، که با معلوم بودن $a$ و $c$ و یک ریشه، ریشهٔ دیگر نیز به سادگی به‌دست می‌آید:

${x^2} + kx + 6 = 0 \Rightarrow $ حاصل ضرب ریشه‌ها $ = \frac{c}{a} \Rightarrow  - 2 \times x = \frac{6}{1}$

$ \Rightarrow  - 2x = 6 \Rightarrow x = \frac{6}{{ - 2}} =  - 3$