درس 2: تابع لگاریتمی و لگاریتم
حسابان (1)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
كدام گزينه درست است؟
1 )
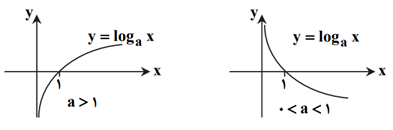
لگاريتم اعداد مثبت كمتر از يک، همواره عددی منفی است.
2 )
تابع لگاریتم $(y={{\log }_{a}}x)$ یک‌به‌یک نیست.
3 )
تابع لگاریتم $(y={{\log }_{a}}x)$ محور $y$ها را قطع می‌کند.
اگر نقطهٔ $(b,d)$ روی نمودار $y={{a}^{x}}$ قرار داشته باشد، آنگاه $(d,b)$ روی نمودار $y={{\log }_{a}}x$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مرتبط
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مرتبط
سوال کنید یا به سوالات دیگران پاسخ دهید ...