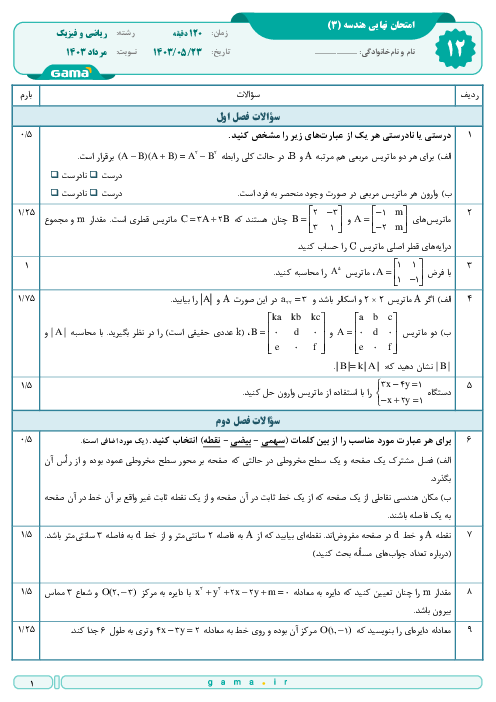
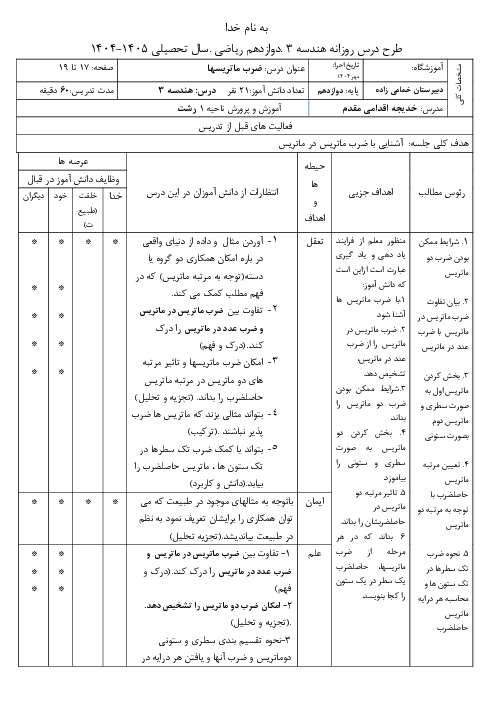
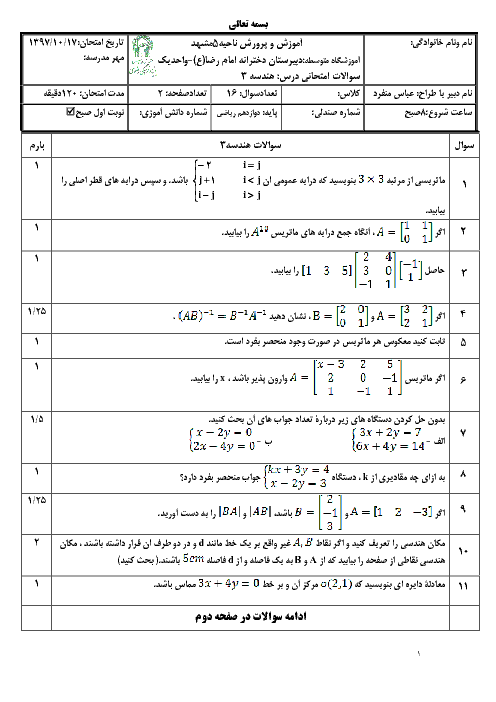
ابتدا ماتریس $A$ را تشکیل می‌دهیم:

${{a}_{11}}={{1}^{2}}-1=0\,,\,{{a}_{12}}={{1}^{2}}-2=-1$

${{a}_{21}}={{2}^{2}}-1=3\,,\,{{a}_{22}}={{2}^{2}}-2=2$

پس ماتریس $A$ به صورت $A=\left[ \begin{matrix}
\begin{matrix}
0  \\
3  \\
\end{matrix} & \begin{matrix}
-1  \\
2  \\
\end{matrix}  \\
\end{matrix} \right]$ خواهد بود.

${{A}^{-1}}=\frac{1}{0\times 2-3(-1)}\left[ \begin{matrix}
\begin{matrix}
2  \\
-3  \\
\end{matrix} & \begin{matrix}
1  \\
0  \\
\end{matrix}  \\
\end{matrix} \right]=\frac{1}{3}\left[ \begin{matrix}
\begin{matrix}
2  \\
-3  \\
\end{matrix} & \begin{matrix}
1  \\
0  \\
\end{matrix}  \\
\end{matrix} \right]\Rightarrow 3{{A}^{-1}}=\left[ \begin{matrix}
\begin{matrix}
2  \\
-3  \\
\end{matrix} & \begin{matrix}
1  \\
0  \\
\end{matrix}  \\
\end{matrix} \right]$

$3{{A}^{-1}}+A+{{I}_{2}}=\left[ \begin{matrix}
\begin{matrix}
2  \\
-3  \\
\end{matrix} & \begin{matrix}
1  \\
0  \\
\end{matrix}  \\
\end{matrix} \right]+\left[ \begin{matrix}
\begin{matrix}
0  \\
3  \\
\end{matrix} & \begin{matrix}
-1  \\
2  \\
\end{matrix}  \\
\end{matrix} \right]+\left[ \begin{matrix}
\begin{matrix}
1  \\
0  \\
\end{matrix} & \begin{matrix}
0  \\
1  \\
\end{matrix}  \\
\end{matrix} \right]=\left[ \begin{matrix}
\begin{matrix}
3  \\
0  \\
\end{matrix} & \begin{matrix}
0  \\
3  \\
\end{matrix}  \\
\end{matrix} \right]$

مجموع درایه‌ها برابر $6$ است.