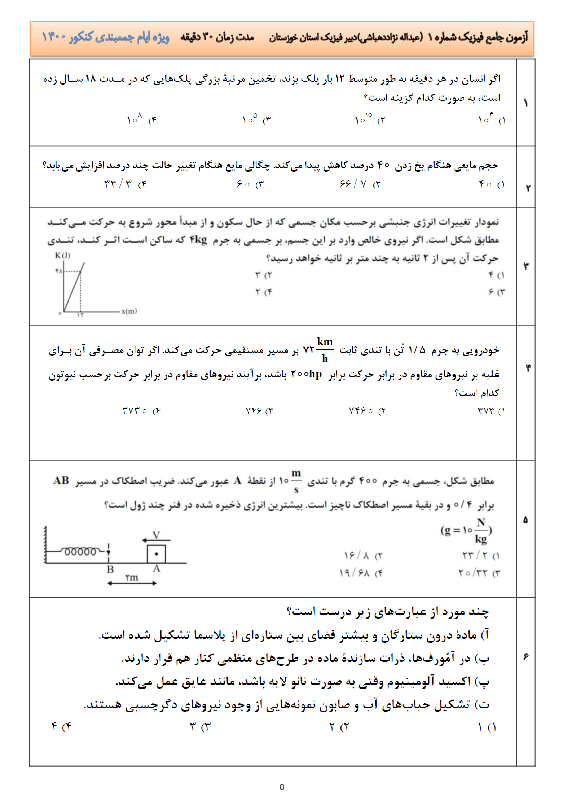
نیروی محرکهٔ القایی متوسط از رابطهٔ $\overline{\varepsilon }=-N\frac{\Delta \Phi }{\Delta t}$ به‌دست می‌آید. در این‌جا چون میدان مغناطیسی در حال تغییر است، تغییر شار از رابطهٔ $\Delta \Phi =\Delta BA\cos \theta $ به‌دست می‌آید. بنابراین نیروی محرکهٔ القایی متوسط برابر است با:

$\overline{\varepsilon }=-N\frac{\Delta BA\cos \theta }{\Delta t}=-N\frac{\Delta B}{\Delta t}A\cos \theta $

با توجه به نمودار $B-T$، میدان مغناطیسی در مدت $40ms$ به طور یکنواخت از $0/8T$ به صفر می‌رسد، بنابراین آهنگ تغییر میدان در هر بازهٔ زمانی از جمله $(0,30ms)$ , برابر است با: 

$\frac{\Delta B}{\Delta t}=\frac{0-0/8}{40\times {{10}^{-3}}}=-20T/s$

و در نتیجه نیروی محرکهٔ القایی متوسط به صورت زیر به دست می‌آید:

$\overline{\varepsilon }=-N\frac{\Delta B}{\Delta t}A\cos \theta $

$=-500\times (-20)\times (40\times {{10}^{-4}})\times \cos 0\Rightarrow \overline{\varepsilon }=40V$