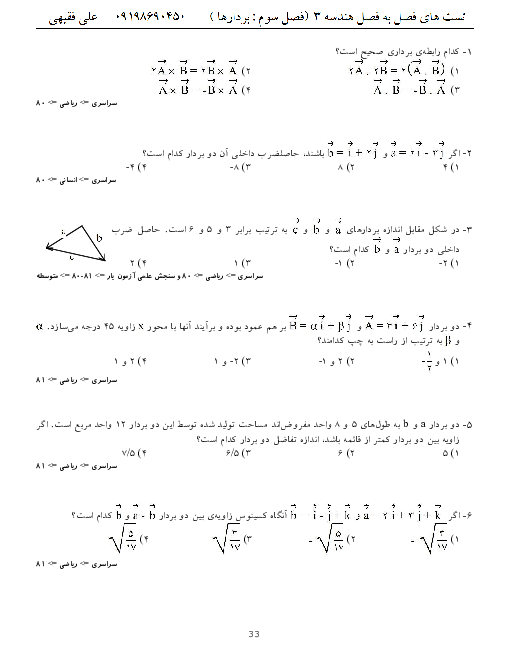
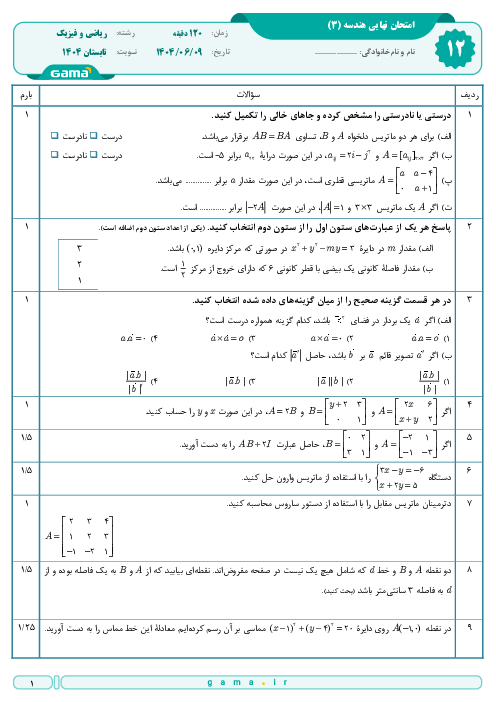
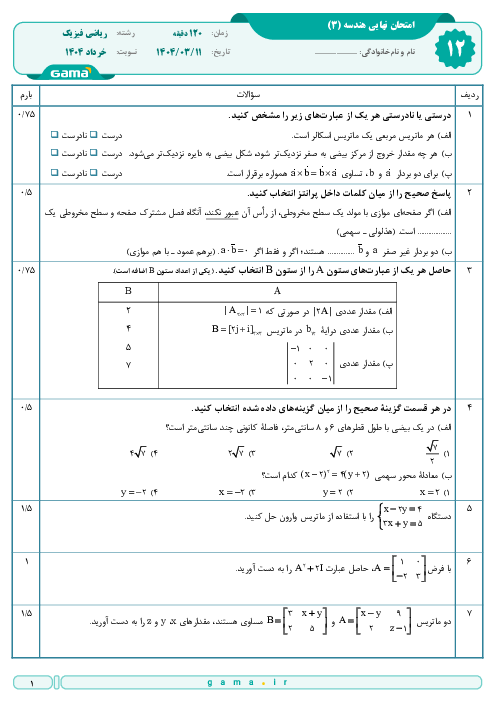
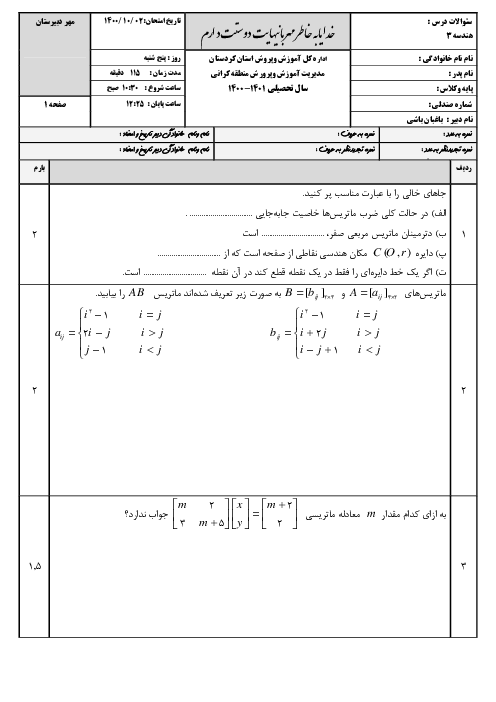
درس 1: ماتریس و اعمال روی ماتریسها
هندسه (3)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
اگر $A={{\left[ {{a}_{ij}} \right]}_{2\times 3}}$، ${{a}_{ij}}=i+j$، $B={{\left[ {{b}_{ij}} \right]}_{2\times 3}}$ و ${{b}_{ij}}=i-j$ باشد، مجموع درایههای ماتریس $C$ از رابطهی $A+B+C=\overline{O}$ چقدر است؟