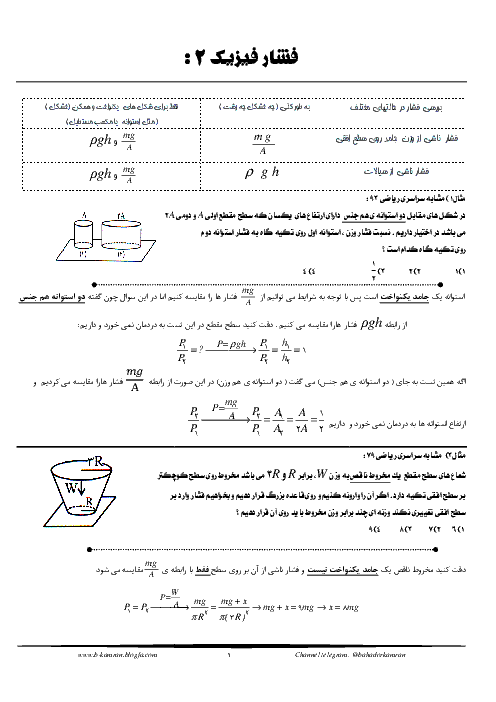
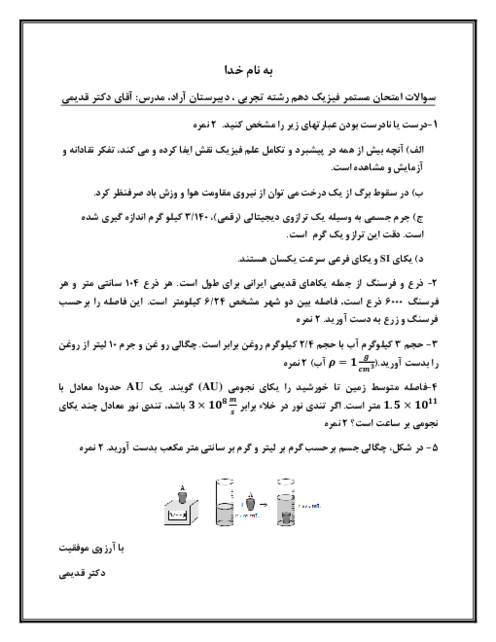
با توجه به متن سؤال داریم:
$\frac{{{N}^{2}}.kg.m}{J.s}$
باید کمیتها از یک جنس باشند تا بتوانیم آنها را با هم جمع بزنیم بنابراین رابطهٔ زیر صادق است:
$\begin{align}
& \left[ {{A}^{2}} \right]=\left[ BC \right]=\left[ \frac{E}{F} \right]=\left[ E \right] \\
& \left[ {{A}^{2}} \right]=\left[ B \right]\left[ C \right]\Rightarrow {{(N.kg)}^{2}}=(\frac{m.s}{J})\left[ C \right]\Rightarrow \left[ C \right]=\frac{{{N}^{2}}.k{{g}^{2}}J}{m.s} \\
\end{align}$
در مورد کمیت $E$ میدانیم که $\left[ \frac{E}{F} \right]=\left[ E \right]$ میباشد بنابراین $F$ یک عدد ثابت است و آن را معادل $1$ در نظر میگیریم.
$\frac{\left[ C \right]}{F}=\frac{{{N}^{2}}.k{{g}^{2}}.J}{m.s}$