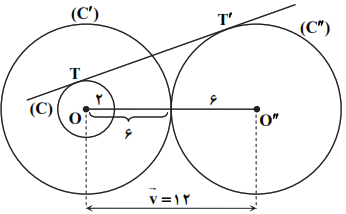
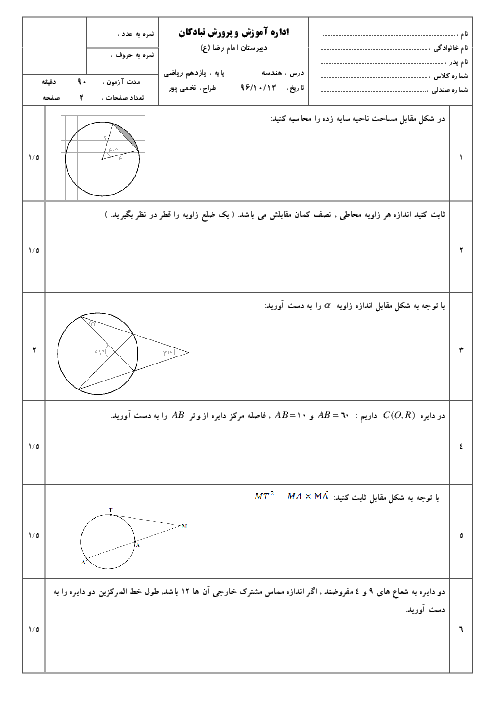
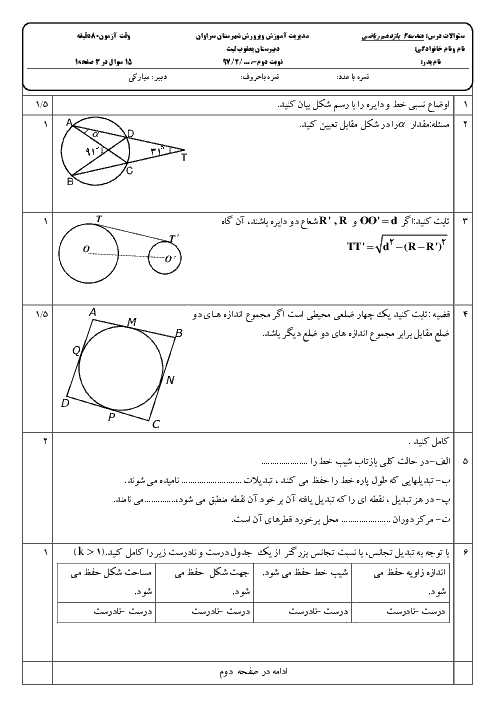
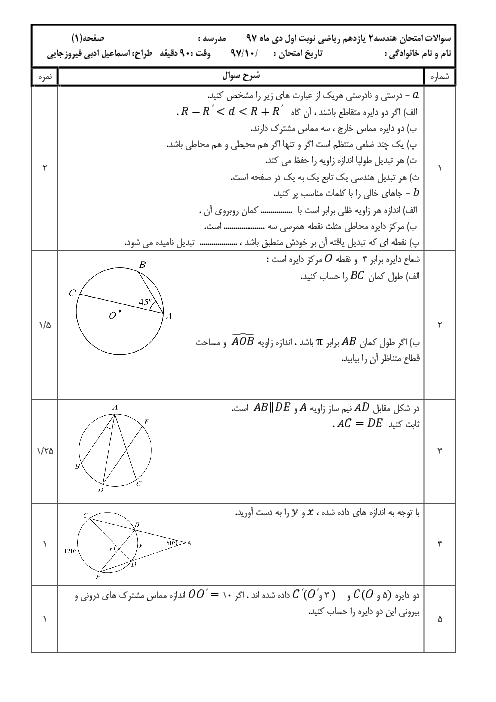
نكته‌ی 1: در تجانس به مركز نقطه‌ی ثابت O و نسبت $k\gt 0$، اگر نقطه‌ی ${A}'$ مجانس نقطه‌ی A در صفحه باشد:

1) A و ${A}'$ و O روی یک خط راست بوده و A و ${A}'$ در یک طرف O هستند.

2) $O{A}'=k.OA$

نکته‌ی 2: در انتقال تحت بردار $\overrightarrow{v}$ اگر ${A}'$ تصویر نقطه‌ی A در صفحه باشد، داریم: $\overrightarrow{A{A}'}=\overrightarrow{v}$

نکته‌ی 3: اندازه‌ی مماس مشترک دو دایره‌ی متخارج $C\left( O,R \right)$ و ${C}'\left( {O}',{R}' \right)$ برابر است با: $\sqrt{O{{{{O}'}}^{2}}-{{\left( R-{R}' \right)}^{2}}}$

ابتدا با توجه به نکات 1 و 2، دایره‌های ${C}'$ و ${C}''$ را مطابق شکل رسم می‌کنیم. واضح است که دایره‌ی ${C}'$ به مرکز O و شعاع 6 است.

زیرا با توجه به نکته‌ی 1، داریم: ${R}'=3\times R=3\times 2=6$

همچنین دایره‌ی ${C}''$ دایره‌ی به مرکز ${O}''$ و شعاع 6 که با دایره‌ی C متخارج است و طول خط‌المرکزین آن‌ها برابر 12 است.

زیرا از طرفی انتقال طولپاست و از طرفی دیگر با توجه به نکته‌ی 2، داریم:

$\overrightarrow{O{O}'}=\overrightarrow{v}\Rightarrow \overrightarrow{O{O}'}=12$

و در نهایت با توجه به نکته‌ی 3، طول مماس مشترک خارجی دو دایره C و ${C}''$ (پاره‌خط $T{T}'$)، برابر است با:

$T{T}'=\sqrt{O{{{{O}'}}^{2}}-{{\left( R-{R}'' \right)}^{2}}}=\sqrt{{{12}^{2}}-{{\left( 2-6 \right)}^{2}}}=\sqrt{144-16}=\sqrt{128}=\sqrt{2\times 64}=8\sqrt{2}$