درس 3: ویژگی‌های لگاریتم و حل معادله‌های لگاریتمی
حسابان (1)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
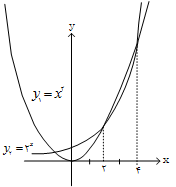
اگر $x\gt 0$ و ${{x}^{2}}\gt {{2}^{x}}$ در بازهٔ $(a,b)$ برقرار باشد، حداکثر مقدار عبارت $\log _{8}^{\sqrt{b-a}}$ کدام است؟
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...