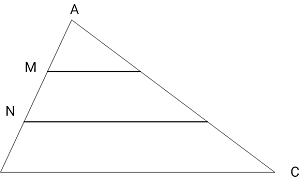
نقاط M,N را روی ضلع AB از مثلث ABC چنان انتخاب میکنیم که با رسم خطوط موازی با BC از این نقاط مثلث را به سه ناحیه با مساحتهای برابر تقسیم کند. $ \frac{AM}{MN} $ چقدر است؟
$ \sqrt{2} +1 $
2 )
$ \sqrt{2} -1 $
3 )
$ \frac{\sqrt{2}}{1+\sqrt{2}} $
4 )
$ \sqrt{2} $