پرتو نور SI مطابق شکل از هوا وارد محیط شفافی به ضخامت 18cm و ضریب شکست می‌شود و پس از بازتاب از سطح آینۀ تختی که در کف محیط دوم قرار دارد، از نقطۀ از محیط دوم خارج… | فیزیک (3) تجربی دوازدهم شماره 218598

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 3: نوسان و امواج فیزیک (3) تجربی دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

پرتو نور SI مطابق شکل از هوا وارد محیط شفافی به ضخامت 18cm و ضریب شکست $\frac{4}{3}$ می‌شود و پس از بازتاب از سطح آینۀ تختی که در کف محیط دوم قرار دارد، از نقطۀ ${O}'$ از محیط دوم خارج می‌شود. این پرتو چند نانو ثانیه پس از ورود به محیط دوم، از آن خارج می‌شود؟ ($3\times {{10}^{8}}\frac{m}{s}$ = تندی نور در هوا، $\sin {{53}^{\circ }}=0/8$)

1 )

2 )

1/5

3 )

4 )

نمایش پاسخ

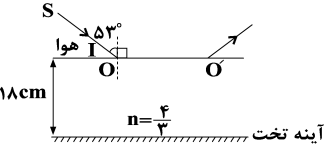
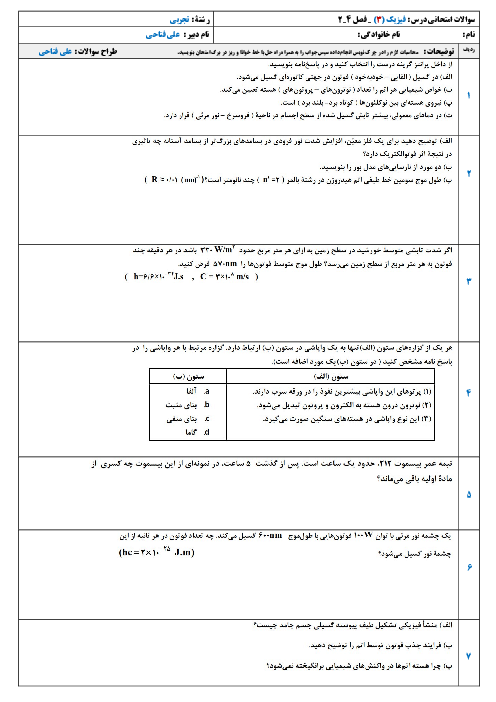
ابتدا مسیر حرکت پرتو را داخل محیط دوم رسم می‌کنیم. با توجه به رابطۀ شکست اسنل داریم:

$\begin{align}
& {{n}_{1}}\sin {{\theta }_{1}}={{n}_{2}}\sin {{\theta }_{2}} \\
& \sin {{53}^{\circ }}=\frac{4}{3}\sin {{\theta }_{2}} \\
& 0/8=\frac{4}{3}\sin {{\theta }_{2}}\Rightarrow \sin {{\theta }_{2}}=0/6\Rightarrow \cos {{\theta }_{2}}=0/8 \\
\end{align}$

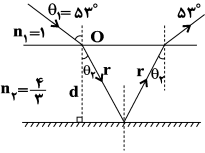
در مثلث قائم‌الزاویۀ ایجاد شده در شکل می‌توان نوشت:

$\cos {{\theta }_{2}}=\frac{d}{r}\Rightarrow r=\frac{18}{0/8}\Rightarrow r=\frac{45}{2}cm$

مسافت طی شده 2r است. پس داریم:

مسافت = 2r = 45cm

اکنون تندی حرکت پرتو داخل محیط دوم را محاسبه می‌کنیم:

$\frac{{{v}_{2}}}{{{v}_{1}}}=\frac{{{n}_{1}}}{{{n}_{2}}}\Rightarrow {{v}_{2}}=\frac{9}{4}\times {{10}^{8}}\frac{m}{s}$

با توجه به رابطۀ تندی می‌توان نوشت:

$t=\frac{مسافت}{تندی}=\frac{45\times {{10}^{-2}}}{\frac{9}{4}\times {{10}^{8}}}=2\times {{10}^{-9}}s=2ns$