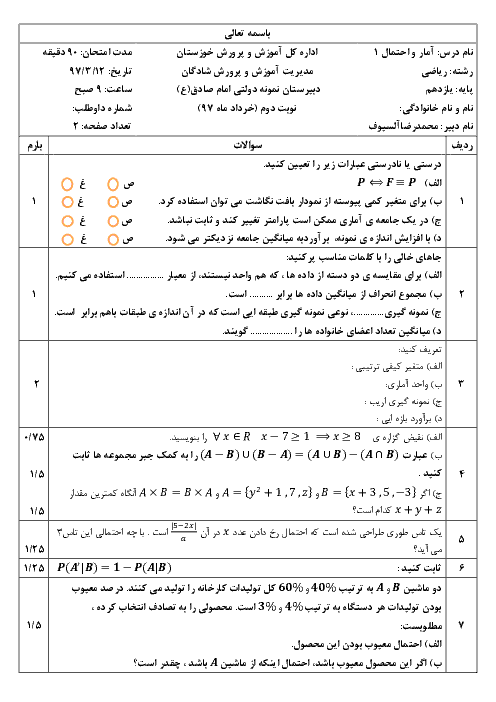
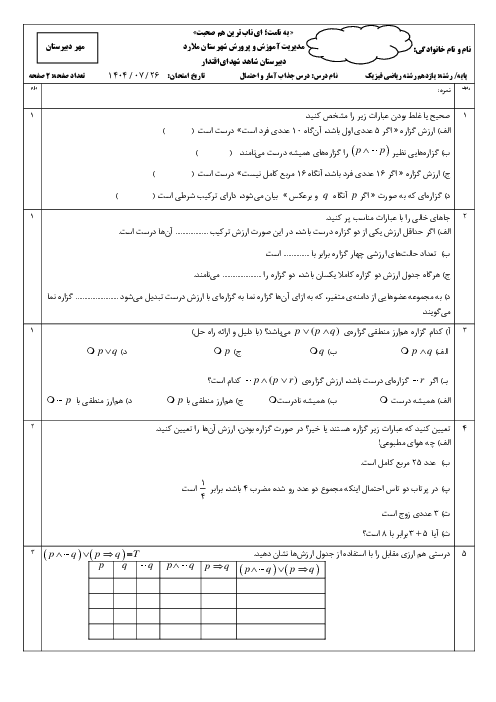
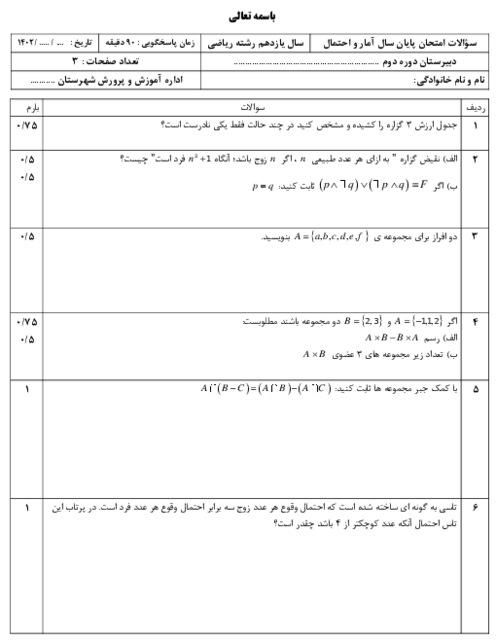
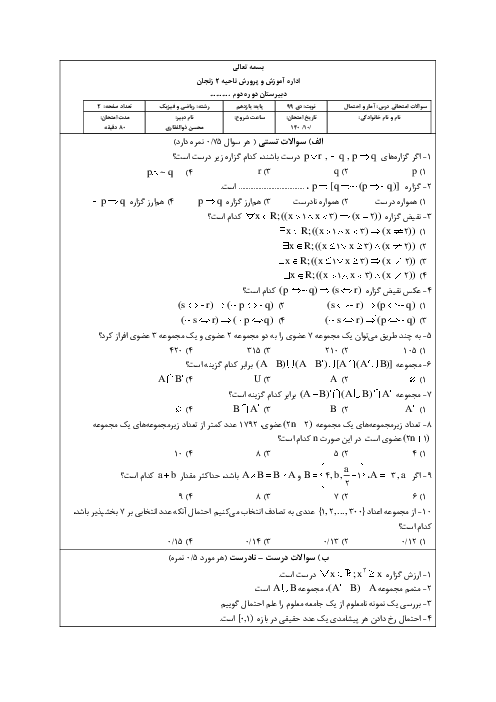
درس 3: قوانین و اعمال بین مجموعه‌ها (جبر مجموعه‌ها)
آمار و احتمال
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
برای دو مجموعهٔ $A=\left( x+y,\frac{9}{100} \right)$ و $B=\left( {{x}^{2}}-{{y}^{2}},\frac{9}{10} \right)$ ، داریم: $A\times B=B\times A$. حاصل $xy$ کدام است؟
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...