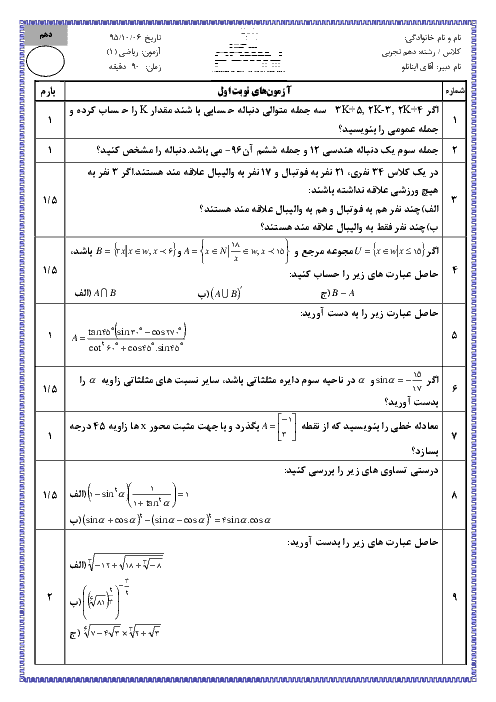
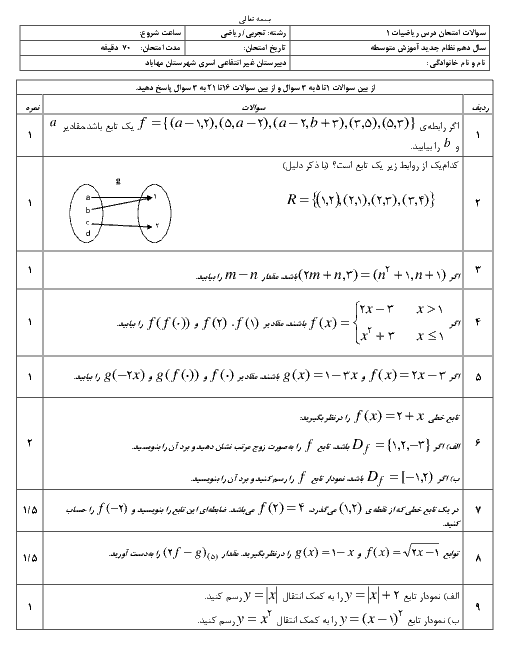
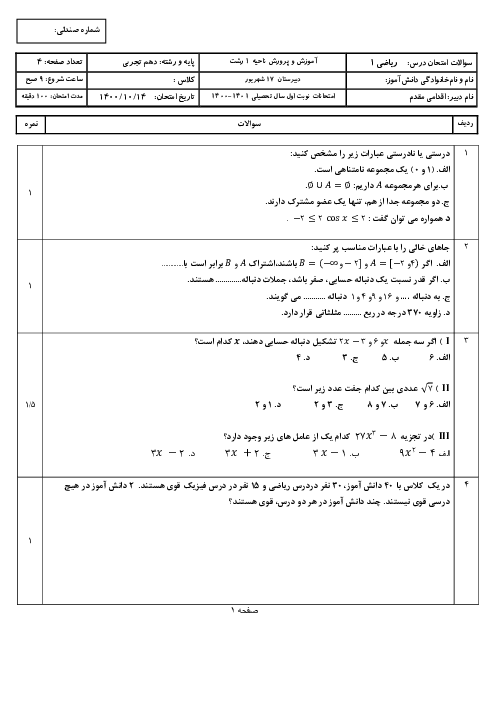
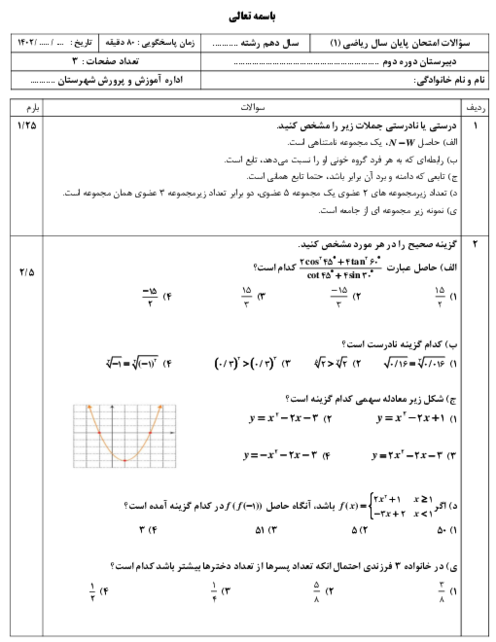
درس 1: مجموعه‌های متناهی و نامتناهی
ریاضی (1)
دهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
اگر $A_n= [-\frac{2}{n}+1 , \frac{2}{n}]$ باشد، نقطه‌ی وسط بازه‌ی $A_1$$\cup$$A_2$ چند برابر نقطه‌ی وسط بازه $A_1$$\cap$$A_2$ می‌باشد؟
تحلیل ویدئویی تست
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...