برای توابع مشتق پذیر $f(x)$ و $g(x)$ در $R$ داریم: ${f}'(x)=(5-x)g(x)$ اگر $g(5)=\frac{-1}{3}$ نقطه‌ای به طول $x=5$ برای تابع چگونه است؟
1 )
ماکزیمم نسبی
مینیمم نسبی
3 )
نقطه‌ای معمولی است.
4 )
قابل تعیین نیست.
پاسخ تشریحی :
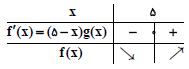
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...