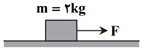
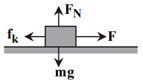
مطابق شكل، در بازهٔ صفر تا ۵ ثانيه (بازهٔ زمانی اعمال نيرو) داريم:
${{F}_{N}}=mg=20N,{{f}_{k}}={{\mu }_{k}}{{F}_{N}}=0/5\times 20=10N$
$F-{{f}_{k}}=ma\Rightarrow 24-10=2a\Rightarrow a=7\frac{m}{{{s}^{2}}}$
مسافت طیشده در 5 ثانیهٔ ابتدایی: $\Delta {{x}_{1}}=\frac{1}{2}a{{t}^{2}}+{{v}_{{}^\circ }}t=\frac{1}{2}(7){{(5)}^{2}}+0=87/5$
سرعت جسم در لحظهٔ $t=5s$: ${{v}_{5s}}=at+{{v}_{{}^\circ }}=(7\times 5)+0=35\frac{m}{s}$
پس از قطع نيرو داريم:
$-{{f}_{k}}=m{a}'\Rightarrow -10=2{a}'\Rightarrow {a}'=-5\frac{m}{{{s}^{2}}}$
در اين قسمت حركت كندشونده است و مسافت طیشده از $t=5s$ تا توقف $(\Delta {{x}_{2}})$ برابر است با:
${{v}^{2}}-v_{{}^\circ }^{2}=2{a}'\Delta {{x}_{2}}\Rightarrow 0-{{35}^{2}}=2(-5)\Delta {{x}_{2}}\Rightarrow \Delta {{x}_{2}}=122/5m$
مسافت کل حرکت: $\ell =\Delta {{x}_{1}}+\Delta {{x}_{2}}=87/5+122/5=210m$