در تابع خطی f داریم: و ، در این صورت نمودار تابع از کدام ناحیهٔ محورهای مختصات عبور نمی‌کند؟ | ریاضی و آمار (1) دهم شماره 245651 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

گام به گام نوبت اول کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

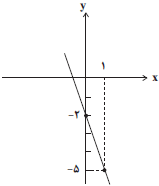
درس 3: نمودار تابع خطی ریاضی و آمار (1) دهم دوره دوم متوسطه- نظری ادبیات و علوم انسانی درسنامه آموزشی این مبحث

در تابع خطی f داریم: $f( - 2) = 4$ و $f(1) = - 5$، در این صورت نمودار تابع $f$ از کدام ناحیهٔ محورهای مختصات عبور نمی‌کند؟

1 )

اول

2 )

دوم

3 )

سوم

4 )

چهارم

نمایش پاسخ

ابتدا ضابطهٔ تابع خطی $f$ را می‌یابیم با فرض $f(x) = mx + n$ داریم:

$f( - 2) = 4 \Rightarrow m \times ( - 2) + n = 4 \Rightarrow - 2m + n = 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$

$f(1) = - 5 \Rightarrow m \times (1) + n = - 5 \Rightarrow m + n = - 5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)$

$(2),(1) \to $

$\eqalign{
& - 2m + n = 4 \cr
& m + n = - 5 \cr} $

$(1) \to \times ( - 1) \to $

$\eqalign{
& 2m - n = - 4 \cr
& m + n = - 5 \cr} $

$3m = - 9 \Rightarrow m = - 3$

حال مقدار $n$ را می‌یابیم:

$m + n = - 5 \to m = - 3 \to - 3 + n = - 5 \Rightarrow n = - 2$

پس ضابطهٔ تابع به فرم $f(x) = - 3x - 2$ است که نمودار آن را رسم می‌کنیم.

همان طور که مشاهده می‌کنید نمودار از ناحیهٔ اول محورهای مختصات عبور نمی‌کند.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1402/03/27

عادل علی پناه

ویدیو دوره آموزشی، ریاضی و آمار (1) دهم دوره دوم متوسطه- نظری

مدرس: مجتبی خالقی

مدت دوره: 7 ساعت (12 فایل)

با آلبوم تست، آزمون دلخواهتو بساز

ترند شده

امتحان ریاضی و آمار 1 انسانی نوبت اول دبیرستان جامی دیماه 1402

4 صفحه

امتحان ریاضی و آمار 1 انسانی نوبت اول دبیرستان جامی دیماه 1402

قدیر عنایت

سوالات امتحان نوبت اول ریاضی و آمار (1) دهم دبیرستان امام خمینی فردیس | دی 1399

3 صفحه

سوالات امتحان نوبت اول ریاضی و آمار (1) دهم دبیرستان امام خمینی فردیس…

مجتبی خالقی

امتحان ترم اول ریاضی و آمار (1) دهم انسانی دبیرستان اندیشه دانشجو | دی 98

3 صفحه

امتحان ترم اول ریاضی و آمار (1) دهم انسانی دبیرستان اندیشه دانشجو | دی…

امتحان دهمی ها

امتحان ریاضی و آمار (1) دهم دبیرستان کوثر | فصل 2 | درس 2: ضابطۀ جبری تابع

3 صفحه

امتحان ریاضی و آمار (1) دهم دبیرستان کوثر | فصل 2 | درس 2: ضابطۀ جبری…

خدیجه اقدامی مقدم

امتحان نوبت اول ریاضی و آمار دهم دبیرستان امام رضا | دی 1397

2 صفحه

امتحان نوبت اول ریاضی و آمار دهم دبیرستان امام رضا | دی 1397

رضا جوانمردی

آزمون نوبت اول ریاضی و آمار (1) دهم دبیرستان خدیجه کبری قائمیه | دی 1398

5 صفحه

آزمون نوبت اول ریاضی و آمار (1) دهم دبیرستان خدیجه کبری قائمیه | دی 1398

الهه فخاریان دارابی…

رایـــــگان

سوالات آزمون نوبت دوم ریاضی و آمار (1) دهم دبیرستان صدرا | شهریور 1401

3 صفحه

سوالات آزمون نوبت دوم ریاضی و آمار (1) دهم دبیرستان صدرا | شهریور 1401

محمدرضا خسروی

نمونه سوال امتحان نوبت شهریور 1401 | ریاضی و آمار (1) دهم انسانی

4 صفحه

نمونه سوال امتحان نوبت شهریور 1401 | ریاضی و آمار (1) دهم انسانی

علی محمدی

آزمون نوبت دوم خرداد 1402 | درس ریاضی و آمار دهم دبیرستان نمونه دولتی حدیث

6 صفحه

آزمون نوبت دوم خرداد 1402 | درس ریاضی و آمار دهم دبیرستان نمونه دولتی…

الهام غلامی پور

امتحان فصل 2 ریاضی و آمار (1) دهم دبیرستان شیخ سلطان احمدی بلده | معادله درجه دوم

2 صفحه

امتحان فصل 2 ریاضی و آمار (1) دهم دبیرستان شیخ سلطان احمدی بلده | معادله…

علیرضا خسروی

موارد بیشتر

موارد بیشتر

ارسال فایل

دلتا را توضیح دهید.

معادله زیر را تجزیه کنید.

عبارت «ما و ما و نصف ما و نصفه‌ای از نصف ما گر تو هم با ما شوی جملگی صد میشویم» یعنی چه؟

موارد بیشتر

ارسال پرسش

موارد بیشتر