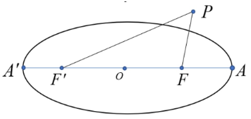
نقطه $P$ بیرون بیضی با قطر بزرگ $AA' = 2a$ و کانونهای $F$ و $F'$ مفروض است.
ثابت کنید:$PF + PF' > 2a$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...