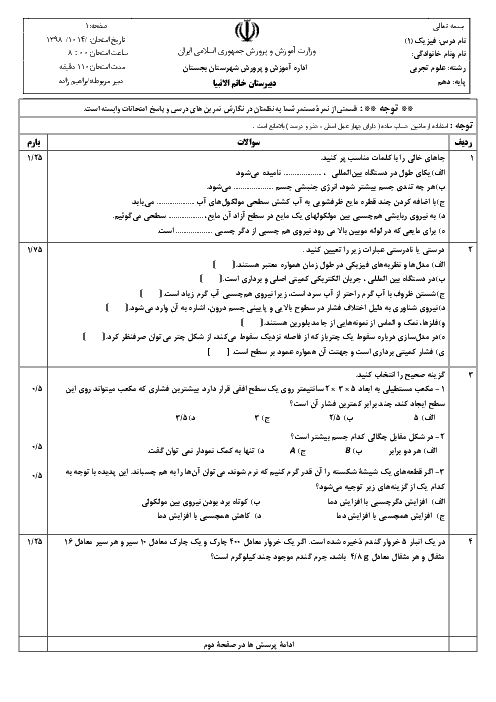
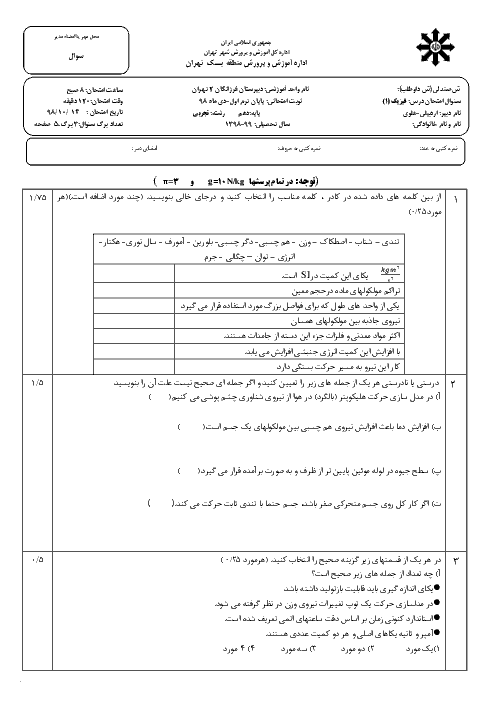
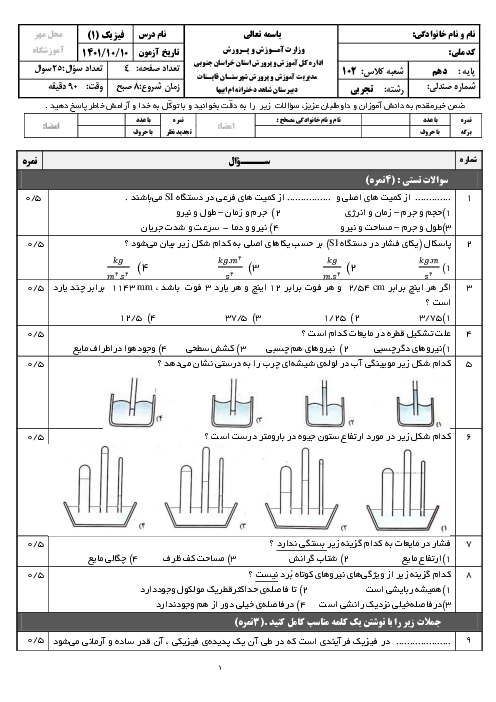
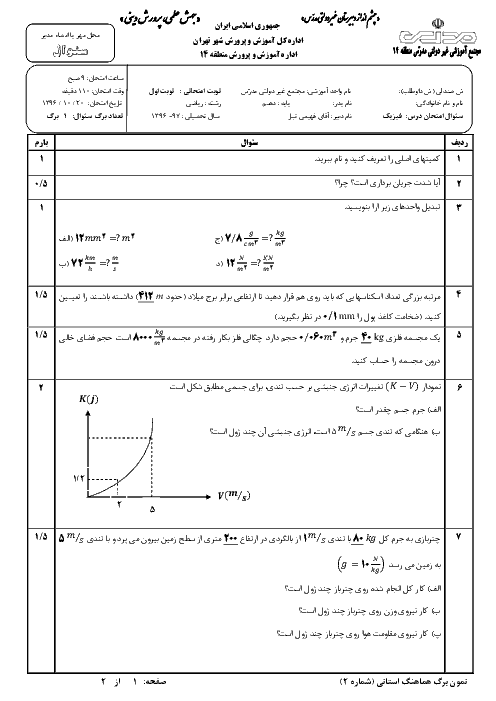
با استفاده از رابطهٔ طول ثانویهٔ یک جسم در اثر تغییر دما و با توجه به داده‌های مسأله داریم:

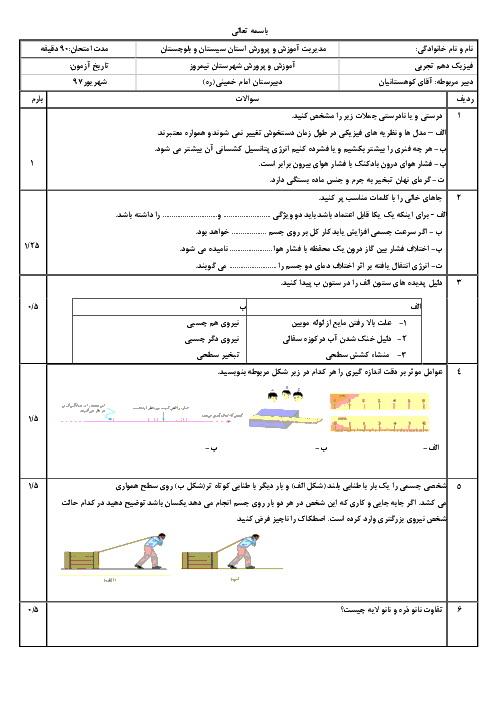
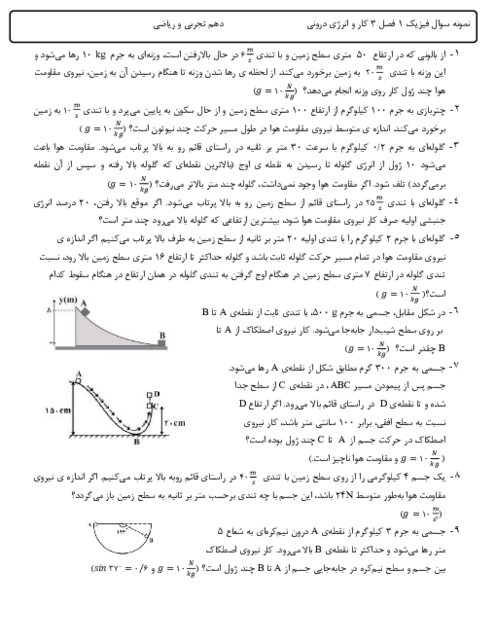
$\left\{ \begin{matrix}
{{l}_{Fe}}={{l}_{0}}_{Fe}(1+{{\alpha }_{Fe}}\Delta \theta )={{l}_{0}}_{Fe}(1+1/2\times {{10}^{-3}})  \\
\Rightarrow {{l}_{Fe}}={{l}_{0}}_{Fe}+1/2\times {{10}^{-3}}{{l}_{0}}_{Fe}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,  \\
{{l}_{Cu}}={{l}_{0}}_{Cu}(1+{{\alpha }_{Cu}}\Delta \theta )={{l}_{0}}_{Cu}(1+1/8\times {{10}^{-3}})  \\
\Rightarrow {{l}_{Cu}}={{l}_{0}}Cu+1/8\times {{10}^{-3}}{{l}_{0}}Cu\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,  \\
\end{matrix} \right.$

با كم‌كردن طرفين رابطه‌ها از هم داريم:

${{l}_{Cu}}-{{l}_{Fe}}={{l}_{0}}_{Cu}-{{l}_{0}}_{Fe}+(1/8{{l}_{0Cu}}-1/2{{l}_{0Fe}})\times {{10}^{-3}}$

$\xrightarrow[{{l}_{Cu}}-{{l}_{Fe}}=0/5mm]{{{l}_{0}}_{Cu}-{{l}_{0Fe}}=-1mm\,\,\,\,(1)}$

$0/5=-1+(1/8{{l}_{0Cu}}-1/2{{l}_{0Fe}})\times {{10}^{-3}}\,\,\,\,\,(2)$

$\xrightarrow{(2),(1)}\left\{ \begin{matrix}
1/8{{l}_{0Cu}}-1/2{{l}_{0Fe}}=1/5\times {{10}^{3}}  \\
{{l}_{0Cu}}={{l}_{0Fe}}-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,  \\
\end{matrix} \right.$

$\to \left\{ \begin{matrix}
{{l}_{0}}_{Fe}=2503mm=2/503m  \\
{{l}_{0Cu}}=2502mm=2/502m  \\
\end{matrix} \right.$