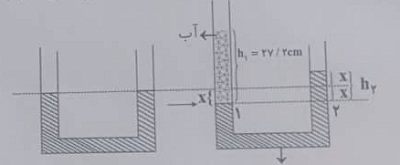
درون لوله‌ی شکلی که جیوه در آن به حالت تعادل قرار دارد، محل سطح آزاد جیوه را روی شاخه‌ها علامت‌ گذاری می‌کنیم. اگر به آرامی در یکی از شاخه‌ها آنقدر آب بریزیم تا…

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

فصل 3: حالت‌های ماده و فشار فیزیک فنی یازدهم دوره دوم متوسطه- فنی صنایع فلزی (صنعت) درسنامه آموزشی این مبحث

درون لوله‌ی $U$ شکلی که جیوه در آن به حالت تعادل قرار دارد، محل سطح آزاد جیوه را روی شاخه‌ها علامت‌ گذاری می‌کنیم. اگر به آرامی در یکی از شاخه‌ها آنقدر آب بریزیم تا ارتفاع ستون آب $27/2cm$ شود، پس از تعادل، سطح جیوه در شاخه‌ی دیگر، نسبت به محل علامت‌ گذاری شده، چند سانتی متر تغییر می‌کند؟ (چگالی جیوه، 13/6 برابر چگالی آب و سطح مقطع لوله در دو طرف لوله یکسان است.)

1 )

0/5

2 )

3 )

4 )

نمایش پاسخ

هر مقدار جیوه از شاخه‌ی سمت چپ پایین بیاید، به همان میزان در شاخه‌ی سمت راست بالا می‌رود.

با استفاده از برابری فشار در نقاط هم‌ تراز یک مایع ساکن، داریم:

${P_1} = {P_2} \Rightarrow \cancel{{{p_0}}} + {\rho _1}\cancel{g}{h_1} = \cancel{{{P_0}}} + {\rho _2}\cancel{g}{h_2} \Rightarrow {\rho _1}{h_1} = {\rho _2}{h_2}$
$\begin{array}{*{20}{c}}
{{\rho _2} = 13/6{\rho _1}}\\
{{h_1} = 27/2cm}
\end{array} \to 27/2\cancel{{{\rho _1}}} = 13/6\cancel{{{\rho _1}}} \times {h_2} \Rightarrow {h_2} = \frac{{27/2}}{{13/6}} = 2cm$

${h_2} = 2x \Rightarrow 2 = 2x \Rightarrow x = 1cm$