اگر و باشد، آنگاه مجموعهٔ چند زیرمجموعه دارد؟ | آمار و احتمال یازدهم شماره 51999

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

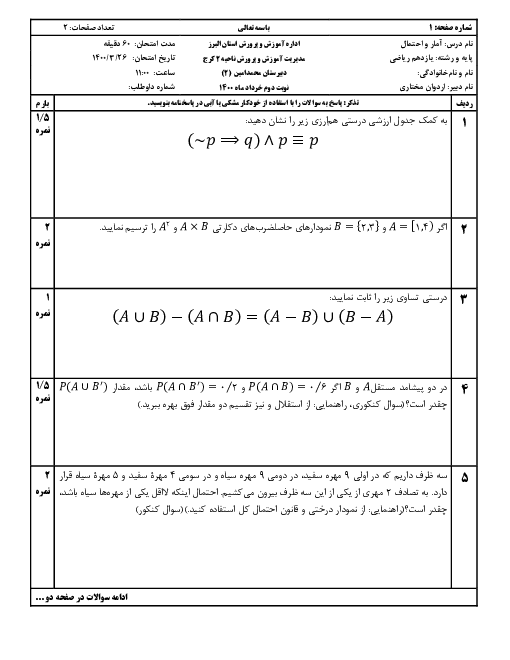
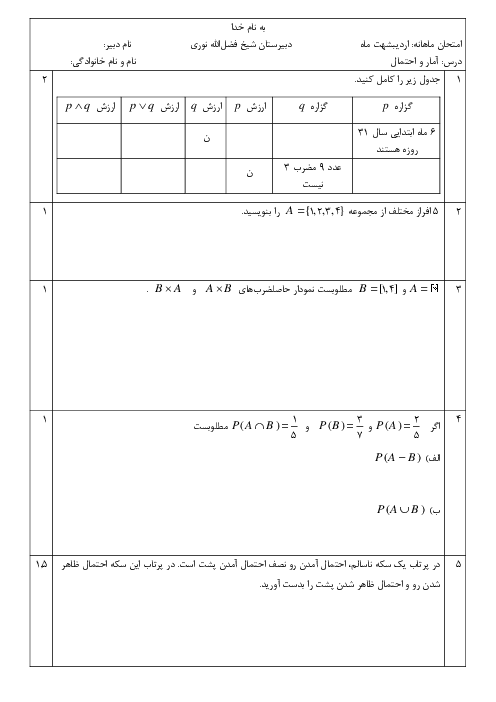
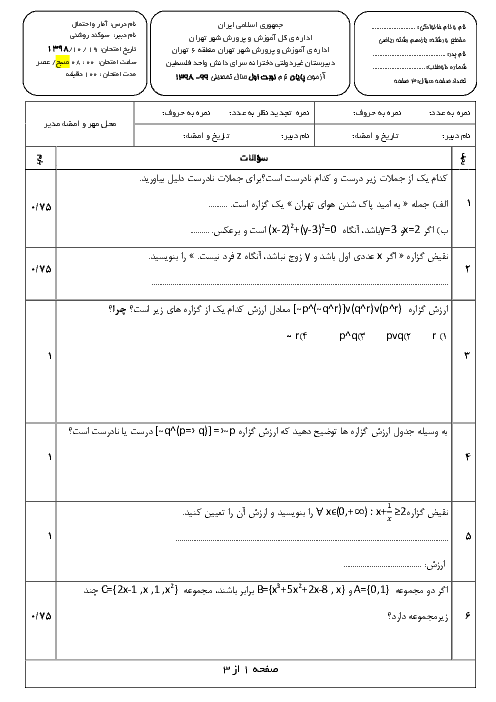
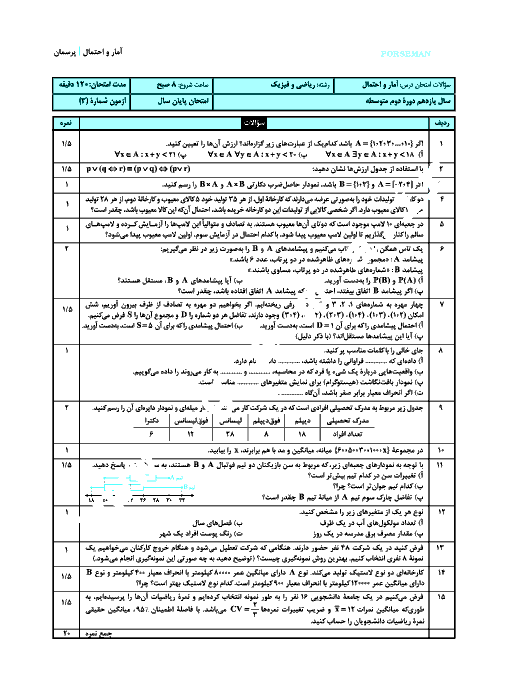
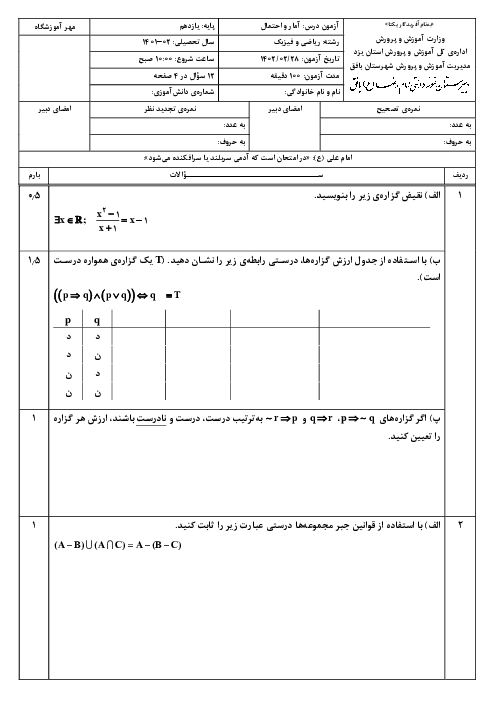
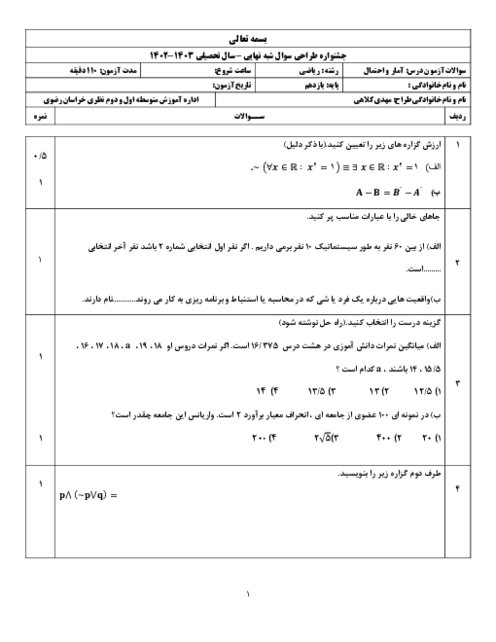
درس 3: قوانین و اعمال بین مجموعه‌ها (جبر مجموعه‌ها) آمار و احتمال یازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

اگر ${{A}_{n}}=\left\{ m\in Z|m\ge -n\,\,\,,\,\,\,{{2}^{m}}\le n \right\}$ و $n\in \mathbb{N}$ باشد، آنگاه مجموعهٔ $({{A}_{3}}-{{A}_{2}})\bigcup {{A}_{1}}$ چند زیرمجموعه دارد؟

1 )

2 )

3 )

4 )

نمایش پاسخ

ابتدا به ازای n=1,2,3، مجموعه‌های ${{A}_{1}}$ ، ${{A}_{2}}$ و ${{A}_{3}}$ را تشکیل می‌دهیم.

$\begin{align} & {{A}_{1}}=\{m\in \mathbb{Z}|m\ge -1,{{2}^{m}}\le 1\}\Rightarrow {{A}_{1}}=\{-1,0\} \\ & {{A}_{2}}=\{m\in \mathbb{Z}|m\ge -2,{{2}^{m}}\le 2\}\Rightarrow {{A}_{2}}=\{-2,-1,0,1\} \\ & {{A}_{3}}=\{m\in \mathbb{Z}|m\ge -3,{{2}^{m}}\le 3\}\Rightarrow {{A}_{3}}=\{-3,-2,-1,0,1\} \\ \end{align}$