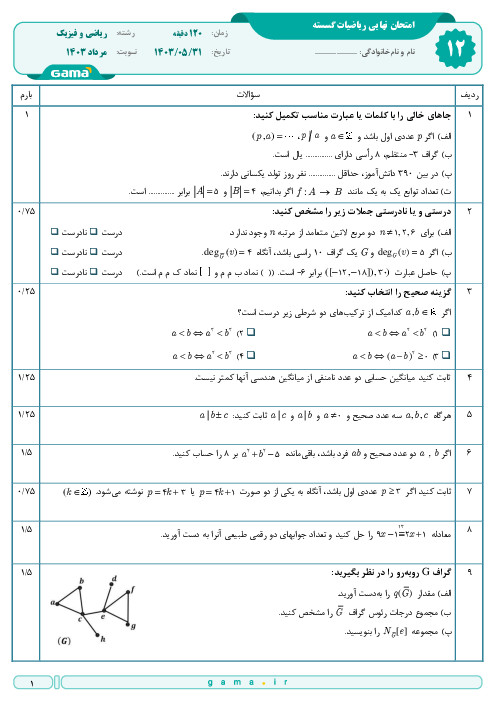
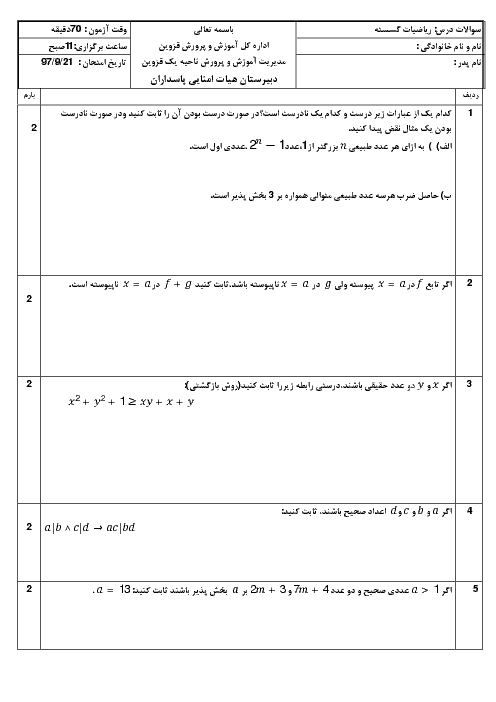
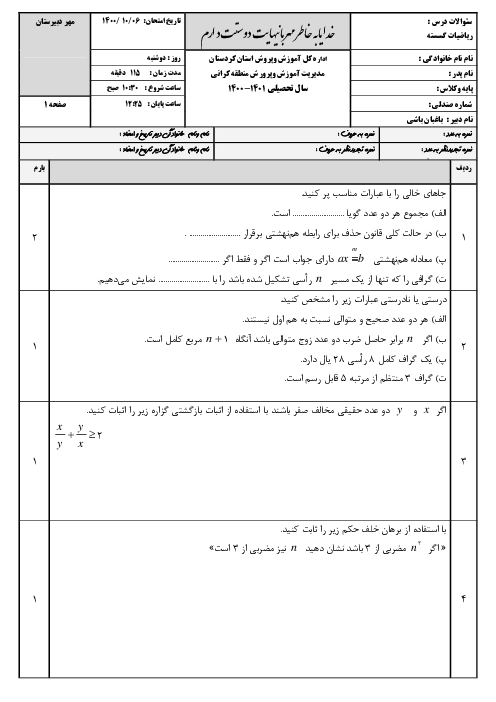
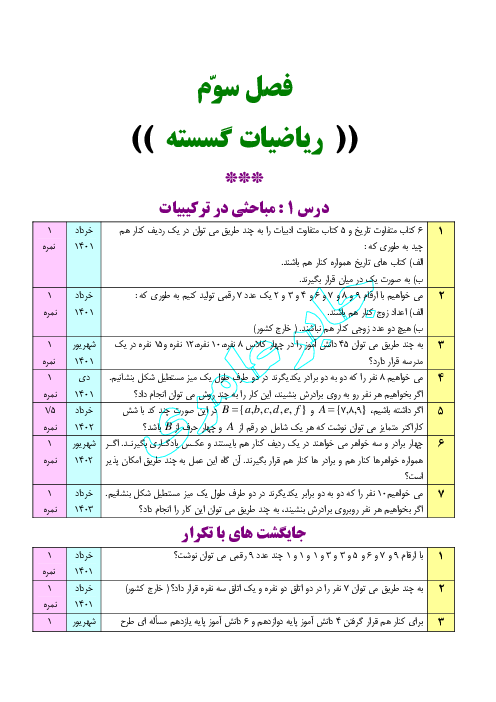
نکته: اگر گزارهٔ مرکب دوشرطی $p\Leftrightarrow q$ درست باشد، گزارههای $p$ و $q$ همارز هستند.
نکته: برای اثبات درستی یک گزاره، گزارههای همارز با آن را درنظر میگیریم و به کمک قوانین ریاضی به گزارٔه اصلی میرسیم. معمولاً این کار به جهت سادهتر شدن اثبات استفاده میشود که به آن روش بازگشتی میگوییم. در روش بازگشتی، خودِ عبارت حکم را ساده میکنیم تا به یک عبارت همیشه درستِ همارز با آن برسیم و در این صورت همۀ مراحل بازگشتپذیر هستند. با توجه به نکتۀ بالا برای عبارت صورتِ سؤال داریم:
$\frac{x}{y}+\frac{y}{x}\ge 2\underset{xy\gt 0}{\overset{\times xy}{\longleftrightarrow}}\,{{x}^{2}}+{{y}^{2}}\ge 2xy\Leftrightarrow {{x}^{2}}-2xy+{{y}^{2}}\ge 0\Leftrightarrow {{(x-y)}^{2}}\ge 0$
پس گزینۀ $1$ پاسخ است.