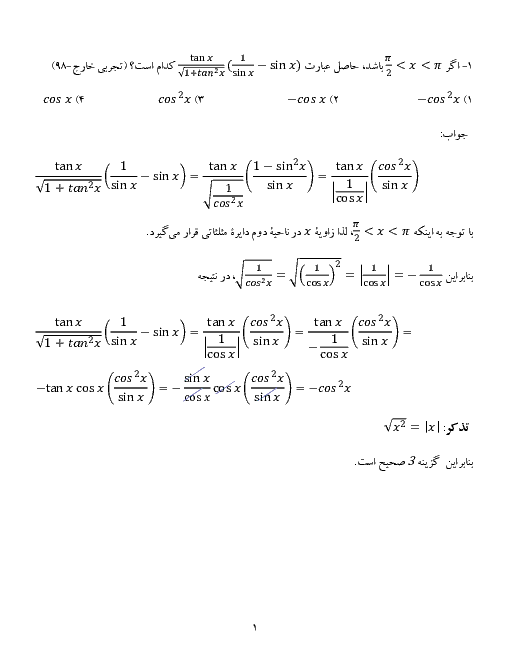
صفرهای تابع $y = 2{x^2} - (m + 2)x + m$ و نقطه تقاطع آن با محور عرض‌ها، رئوس یک مثلث هستند. اگر مساحت این مثلث برابر $\frac{3}{4}$ باشد، کدام می‌تواند طول رأس سهمی $y = {x^2} - mx + 1$ باشد؟
1 )
$\frac{1}{4}$
2 )
$\frac{2}{3}$
3 )
$ - \frac{3}{4}$
$ - \frac{1}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...