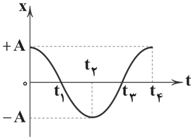
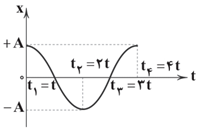
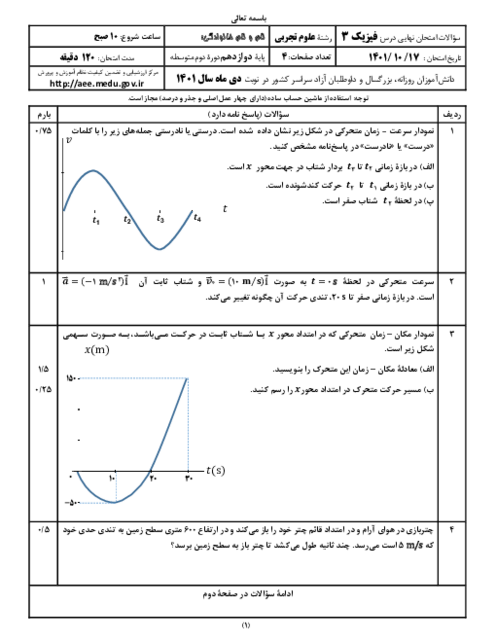می‌دانیم که تابع کسینوسی، تابع متناوبی است که در بازه‌های متقارن بین دو مقدار مشخص $\pm A$ تغییر می‌کند. به بیان دیگر از صفر تا ${{t}_{1}}$ برابر ${{t}_{1}}$ تا ${{t}_{2}}$ و برابر ${{t}_{2}}$ تا ${{t}_{3}}$ و برابر ${{t}_{3}}$ تا ${{t}_{4}}$ می‌باشد.

${{t}_{1}}-0={{t}_{2}}-{{t}_{1}}={{t}_{3}}-{{t}_{2}}={{t}_{4}}-{{t}_{3}}=t$

بردار سرعت متوسط از صفر تا ${{t}_{1}}$ به صورت زیر است:

${{t}_{1}}$ صفر تا: ${{v}_{av}}=\frac{\Delta x}{\Delta t}=\frac{0-(+A)}{{{t}_{1}}-0}=\frac{-A}{t}\Rightarrow {{\overrightarrow{v}}_{av}}=-\frac{A}{t}\overrightarrow{i}$

بردار سرعت متوسط در هر یک از گزینه‌ها برابر است با:

1) ${{t}_{2}}$ تا ${{t}_{1}}$: ${{v}_{1av}}=\frac{\Delta x}{\Delta t}=\frac{-A-(0)}{{{t}_{2}}-{{t}_{1}}}=\frac{-A}{2t-t}\Rightarrow {{\overrightarrow{v}}_{1av}}=\frac{-A}{t}\overrightarrow{i}$

2) ${{t}_{3}}$ صفر تا: ${{v}_{2av}}=\frac{\Delta x}{\Delta t}=\frac{0-(+A)}{{{t}_{3}}-0}=\frac{-A}{3t}\Rightarrow {{\vec{v}}_{2av}}=\frac{-A}{3t}\vec{i}$

3) ${{t}_{4}}$ تا ${{t}_{2}}$: ${{v}_{3av}}=\frac{\Delta x}{\Delta t}=\frac{+A-(-A)}{{{t}_{4}}-{{t}_{2}}}=\frac{2A}{2t}\Rightarrow {{\vec{v}}_{3av}}=\frac{+A}{t}\vec{i}$

4) ${{t}_{3}}$ تا ${{t}_{1}}$: ${{v}_{4av}}=\frac{\Delta x}{\Delta t}=\frac{0-0}{{{t}_{3}}-{{t}_{1}}}=0$

پس ${{\overrightarrow{v}}_{3av}}=-{{\overrightarrow{v}}_{av}}$ است و می‌بایست گزینه‌ی (3) را انتخاب کنیم.