درس 2: مشتق‌پذیری و پیوستگی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
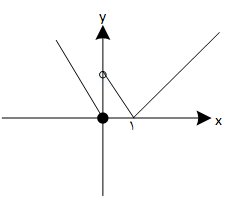
كدام گزينه در مورد تابع x$f(x)\left\{ _{-x,x\le 0}^{\left| x-1 \right|,x\rangle 0} \right.$ صحيح است؟
1 )
تابع در $x=0$ مشتق‌پذیر است.
تابع در فاصله‌ی $\left( -\infty ,0 \right]$ مشتق‌پذیر است.
3 )
${{{f}'}_{-}}(0)={{{f}'}_{+}}(0)=-1$ است.
4 )
تابع در فاصله‌ی $(0,+\infty )$ مشتق‌پذیر است.
پاسخ تشریحی :
تحلیل ویدئویی تست
امیرحسین مزدور 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...