در شکل زیر اگر بارهای الکتریکی نقطه‌ای در رأس‌های مربع در جهت پاد ساعتگرد حرکت کنند و در وسط اضلاع مربع قرار گیرند، اندازهٔ نیروی خالص وارد بر باری که در مرکز مربع…

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 1: الکتریسیتۀ ساکن فیزیک (2) یازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

در شکل زیر اگر بارهای الکتریکی نقطه‌ای در رأس‌های مربع در جهت پاد ساعتگرد حرکت کنند و در وسط اضلاع مربع قرار گیرند، اندازهٔ نیروی خالص وارد بر باری که در مرکز مربع قرار دارد چند برابر می‌شود و زاویهٔ بردار آن چند درجه تغییر می‌کند؟

1 )

2، ${{45}^{{}^\circ }}$

2 )

2، ${{90}^{{}^\circ }}$

3 )

4، ${{45}^{{}^\circ }}$

4 )

4، ${{90}^{{}^\circ }}$

نمایش پاسخ

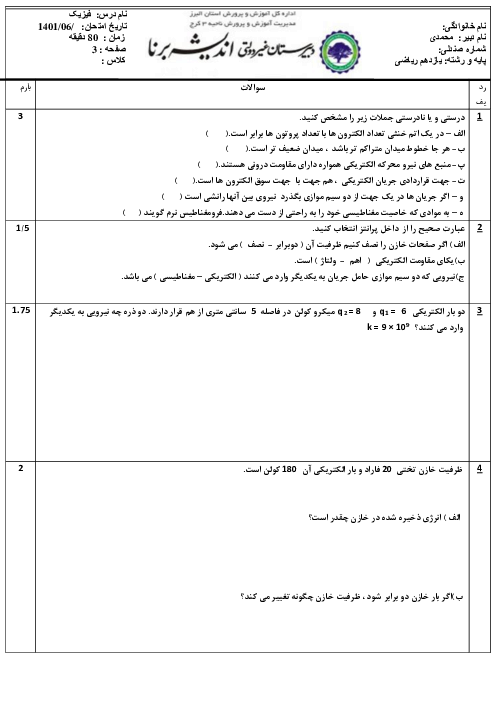
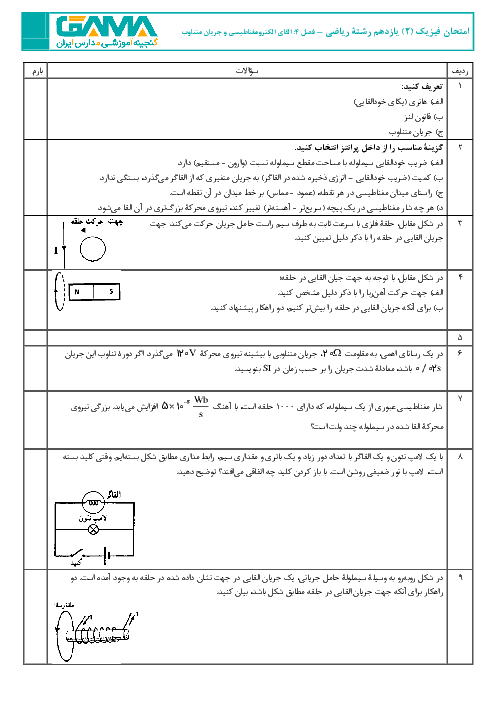
در حالت اول ابتدا نیروی خالص وارد بر بار q در مرکز مربع را می‌یابیم، دقت کنید اندازهٔ همهٔ بارها یکسان و فاصلهٔ آن‌ها از باری که در مرکز مربع قرار دارد نیز یکسان است. پس در این حالت اندازهٔ نیرویی که بار q در رأس مربع به بار q در مرکز مربع وارد می‌کند را F در نظر می‌گیریم:
با توجه به تصویر 1
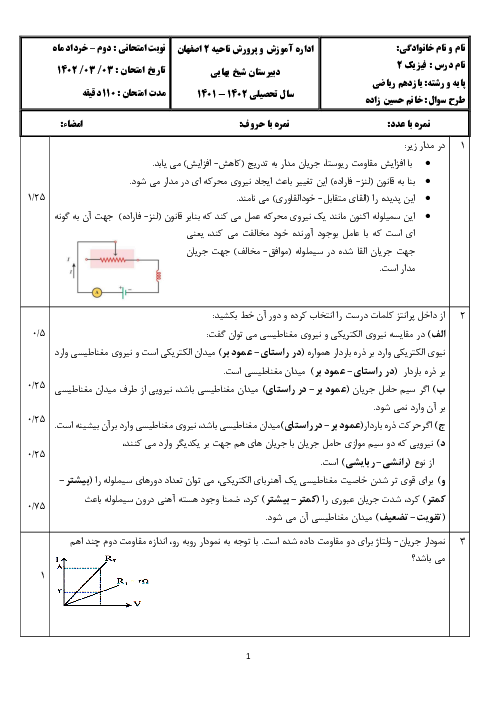
در حالت دوم دقت کنید فاصلهٔ بارها از بار q تغییر کرده است. ابتدا اندازهٔ نیروی وارد از طرف هر بار بر بار q در مرکز را ${F}'$ در نظر می‌گیریم، داریم:
با توجه به تصویر 2
پس جهت بردار نیروی خالص ${{45}^{{}^\circ }}$ تغییر کرده است و داریم:

$\frac{{{{{F}'}}_{T}}}{{{F}_{T}}}=\frac{2\sqrt{2}{F}'}{2\sqrt{2}F}=\frac{{{F}'}}{F}=\frac{\frac{k{{q}^{2}}}{{{(\frac{d}{2})}^{2}}}}{\frac{k{{q}^{2}}}{{{(\frac{\sqrt{2}d}{2})}^{2}}}}=2$