نمودار تعداد هسته‌های پرتوزا برحسب زمان برای دو نمونۀ و مطابق شكل زير است. نيمه‌عمر مادهٔ چند شبانه‌روز است؟ | فیزیک (3) ریاضی دوازدهم شماره 86107

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 2: پرتوزایی طبیعی و نیمه عمر فیزیک (3) ریاضی دوازدهم متوسطه دوم نظری علوم ریاضی درسنامه آموزشی این مبحث

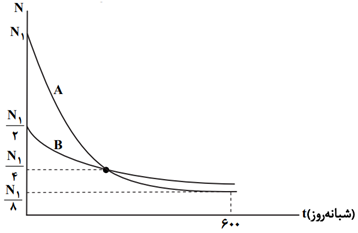
نمودار تعداد هسته‌های پرتوزا برحسب زمان برای دو نمونۀ $A$ و $B$ مطابق شكل زير است. نيمه‌عمر مادهٔ $B$ چند شبانه‌روز است؟

1 )

600

2 )

400

3 )

300

4 )

200

نمایش پاسخ

محل برخورد دو منحنی زمانی را نشان می‌دهد كه تعداد هسته‌های $A$ به $\frac{1}{4}$ مقدار اوليه (دو نيمه‌عمر) و تعداد هسته‌های $B$ به $\frac{1}{2}$ مقدار اوليه (يک نيمه‌عمر) رسيده است.

بنابراين اگر نيمه‌عمر نمونۀ $A$ را با ${{T}_{A}}$ و نيمه‌عمر نمونۀ $B$ را با ${{T}_{B}}$ نمايش دهيم، داريم: $2{{T}_{A}}={{T}_{B}}$

از سوی ديگر ۶۰۰ شبانه‌روز مدتی است كه تعداد هسته‌های پرتوزای $A$ به $\frac{1}{8}$ مقدار اوليه می‌رسد و در اين صورت $\Delta t=3{{T}_{A}}$ است.

$3{{T}_{A}}=600\Rightarrow {{T}_{A}}=200\Rightarrow {{T}_{B}}=400$ شبانه‌روز

گزارش اشکال