درس 2: تابع درجه سوم، توابع یکنوا و بخش‌پذیری و تقسیم
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
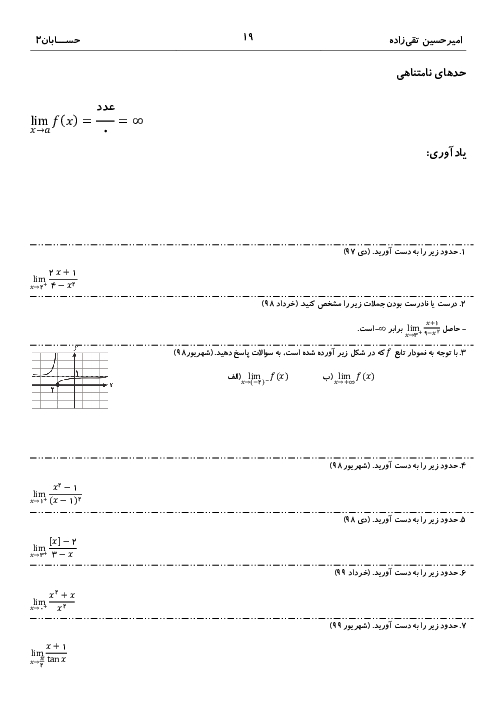
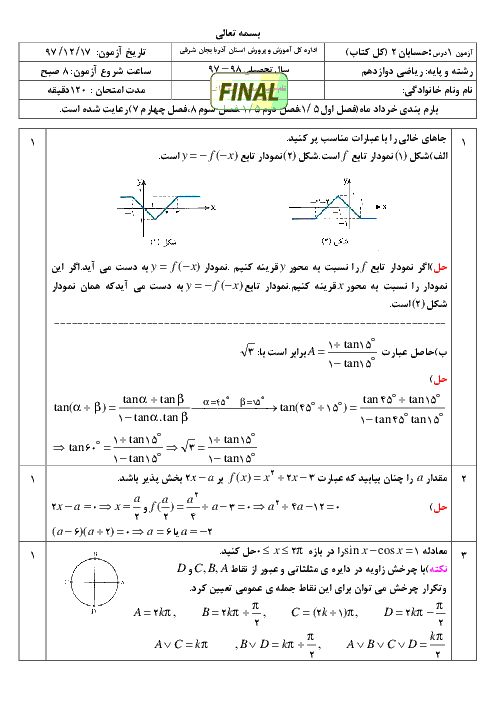
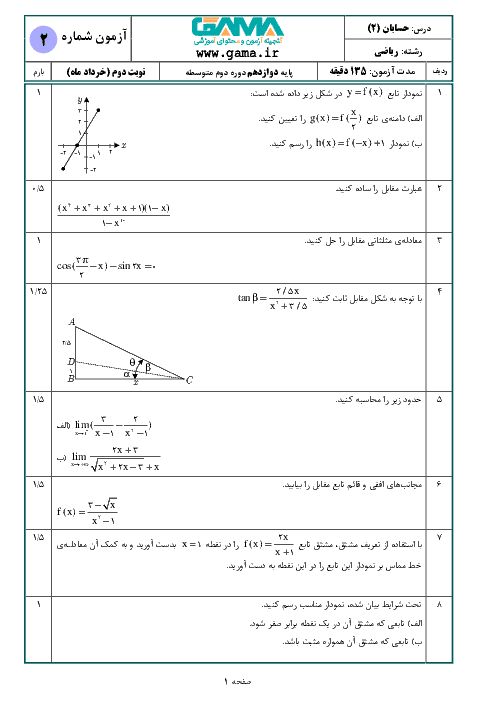
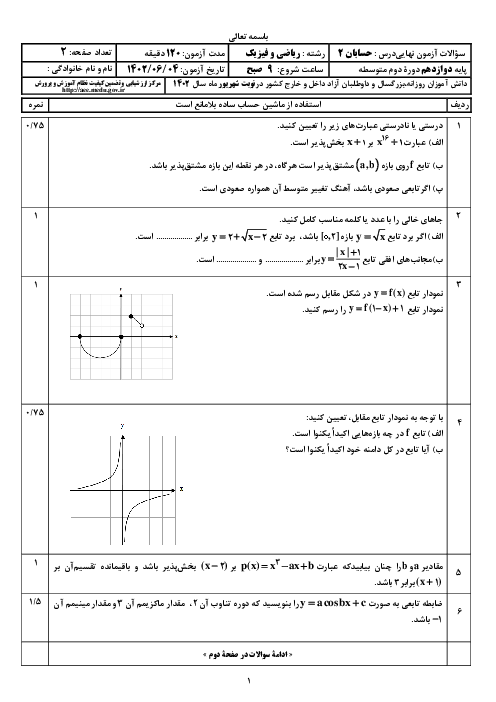
تابع $f\left( x \right)=\left| \sin x \right|$ مفروض است. در کدام یک از بازه‌های زیر، به ازای هر ${{x}_{1}}$ و ${{x}_{2}}$ عضو این بازه، رابطه‌ی ${{x}_{1}}\lt{{x}_{2}}\Rightarrow f\left( {{x}_{1}} \right)\gt f\left( {{x}_{2}} \right)$ برقرار است؟
1 )
$\left( \frac{\pi }{2},\frac{3\pi }{2} \right)$
2 )
$\left( -\frac{\pi }{2},\frac{\pi }{2} \right)$
$\left[ -\frac{\pi }{2},0 \right]$
4 )
$\left[ 0,\frac{\pi }{2} \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...