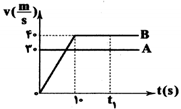
اتومبیل $A$ در لحظه‌ی $t=۰$ با سرعت $۳۰\frac{m}{s}$ از کنار یک ساختمان می‌گذرد و با سرعت ثابت به حرکت خود ادامه می‌دهد. در همان زمان، اتومبیل $B$ از همان مکان، از حال سکون و با شتاب ثابت $۴\frac{m}{{{s}^{۲}}}$ به حرکت در می‌آید.  اتومبیل $B$ به مدت ۱۰ ثانیه با این شتاب حرکت کرده و سپس با سرعت ثابت به حرکت خود ادامه می‌دهد. در فاصله‌ی چند متری از ساختمان دو اتومبیل به هم می‌رسند؟