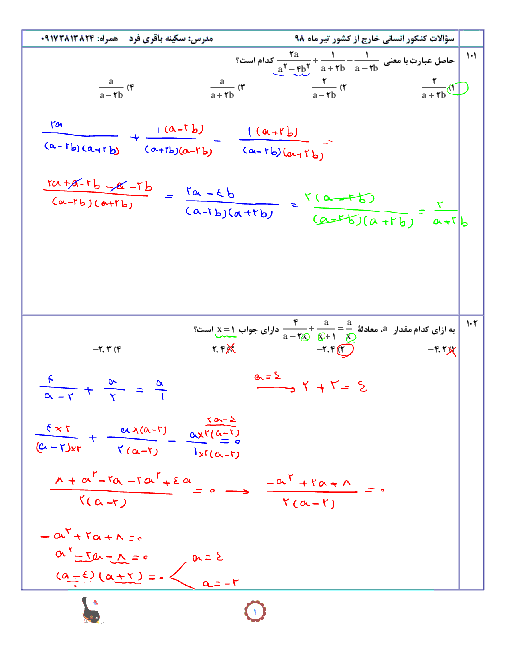
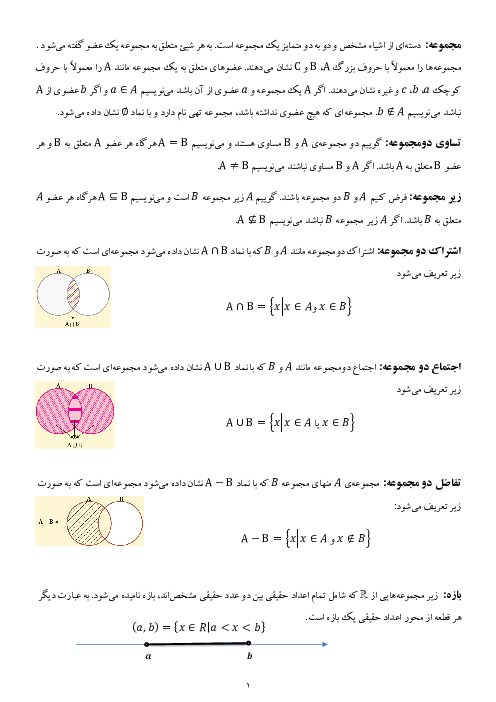
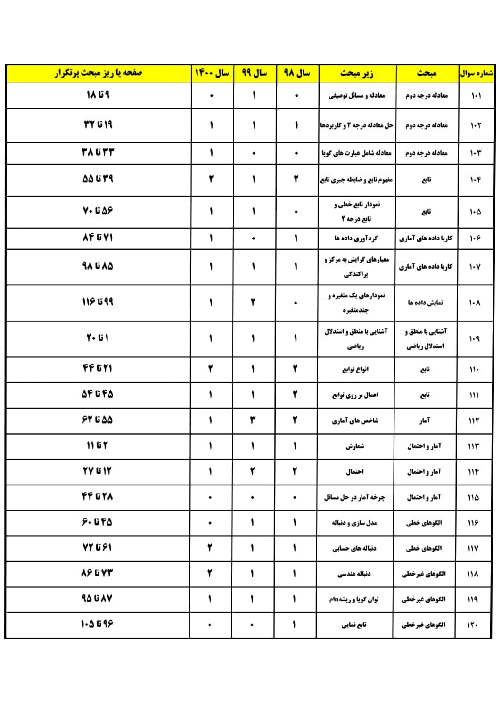
اگر $f(x)={{x}^{2}}-1$ و $g(x)=x+1$ باشند، دامنه و ضابطهٔ تابع $\frac{f}{g}$ کدام است؟
1 )
$\left\{ \begin{align} & (\frac{f}{g})(x)=x-1 \\ & {{D}_{\frac{f}{g}}}=R-\{1\} \\ \end{align} \right.$
$\left\{ \begin{align} & (\frac{f}{g})(x)=x-1 \\ & {{D}_{\frac{f}{g}}}=R-\{-1\} \\ \end{align} \right.$
3 )
$\left\{ \begin{align} & (\frac{f}{g})(x)=\frac{{{x}^{2}}-1}{x+1} \\ & {{D}_{\frac{f}{g}}}=R \\ \end{align} \right.$
4 )
$\left\{ \begin{align} & (\frac{f}{g})(x)=\frac{{{x}^{2}}-1}{x+1} \\ & {{D}_{\frac{f}{g}}}=R-\{\pm 1\} \\ \end{align} \right.$
پاسخ تشریحی :
تحلیل ویدئویی تست
عادل علی پناه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...