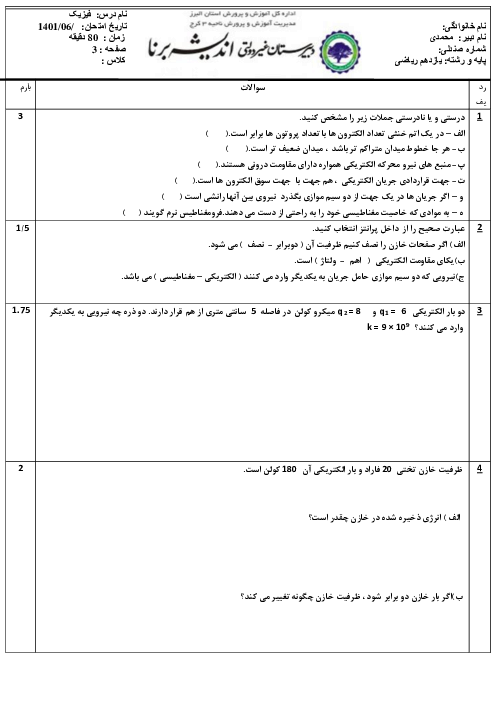
در دمای ثابت، مقاومت يک سيم فقط به ويژگی‌های فيزيكی آن وابسته است. با توجّه به اين‌كه تنها قطر سيم تغيير كرده است، داريم:

$R=\rho \frac{L}{A}\Rightarrow \frac{{{R}_{2}}}{{{R}_{1}}}=\frac{{{A}_{1}}}{{{A}_{2}}}={{(\frac{{{D}_{1}}}{{{D}_{2}}})}^{2}}\xrightarrow{{{D}_{2}}=2{{D}_{1}}}\frac{{{R}_{2}}}{{{R}_{1}}}=\frac{1}{4}$

حالا با استفاده از قانون اهم و در نظر گرفتن اين نكته كه ولتاژ ثابت است، می‌توان نوشت:

$I=\frac{V}{R}\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}=\frac{{{R}_{2}}}{{{R}_{1}}}\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}=\frac{1}{4}$

بنابراين تعداد الكترون‌های عبوری از هر مقطع سيم در بازه‌های زمانی يكسان، برابر است با:

$I=\frac{\vartriangle q}{\vartriangle t}=\frac{ne}{\vartriangle t}\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}=\frac{{{n}_{1}}}{{{n}_{2}}}\Rightarrow \frac{{{n}_{1}}}{{{n}_{2}}}=\frac{1}{4}$