به بررسی گزاره‌ها می‌پردازیم:

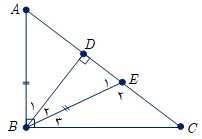
چون $AB = BE$، بنابراین مثلث ABE متساوی‌الساقین است، پس $\hat A = {\hat E_1}$ و گزارهٔ «الف» درست است.

می‌دانیم در مثلث متساوی‌الساقین ارتفاع وارد بر قاعده، میانه نیز هست.

$\mathop {ADB}\limits^\Delta  ,\mathop {BDE}\limits^\Delta   \Rightarrow \left\{ {\begin{array}{*{20}{c}}
  {AD = DE} \\ 
  {BD = BD} \\ 
  {{{\hat D}_1} = {{\hat D}_2} = {{90}^ \circ }} 
\end{array}} \right. \to \mathop {ADB}\limits^\Delta   \cong \mathop {BDE}\limits^\Delta  $

بنابراین گزارهٔ «ج» درست است.

از طرفی در مثلث BDC خواهیم داشت:

${\hat B_2} + {\hat B_3} + \hat C + {\hat D_1} = {180^ \circ } \Rightarrow {\hat B_2} + {\hat B_3} + \hat C + {90^ \circ } = {180^ \circ }$

${\hat B_2} + {\hat B_3} + \hat C = {90^ \circ }\xrightarrow{{{{\hat B}_1} + {{\hat B}_2} + {{\hat B}_3} = {{90}^ \circ }}}{90^ \circ } - {\hat B_1} + \hat C = {90^ \circ } \Rightarrow \hat C = {\hat B_1}$

بنابراین گزارهٔ «ب» درست است.