نسبت مساحت‌ها $ = \frac{2}{5} \Rightarrow $ نسبت تشابه $ = {(\frac{2}{5})^2} = \frac{4}{{25}}\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$

مساحت لوزی کوچک $ = \frac{{\mathop {\cancel{8}}\limits^4  \times \sqrt {80} }}{{\mathop {\cancel{2}}\limits_1 }} = 4\sqrt {80}  = 4 \times 4\sqrt 5  = 16\sqrt 5 \,\,\,\,\,\,\,\,\,(2)$

مساحت لوزی بزرگ برابر است با:

$(2),(1) \Rightarrow \frac{{16\sqrt 5 }}{x} = \frac{4}{{25}} \Rightarrow \cancel{4}x = 25 \times \mathop {\cancel{{16}}}\limits^4 \sqrt 5  \Rightarrow x = 100\sqrt 5 $

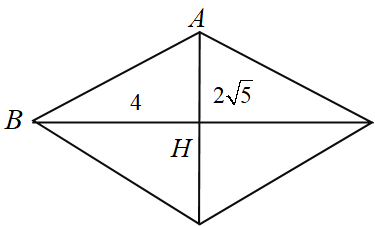
در لوزی کوچک، می‌دانیم:

$\sqrt {80}  = 4\sqrt 5 $
$\mathop {ABH}\limits^\Delta  :A{B^2} = A{H^2} + B{H^2}$
$ \Rightarrow A{B^2} = {(2\sqrt 5 )^2} + {(4)^2}$
$ = 20 + 16 = 36 \Rightarrow AB = 6$

با استفاده از تشابه دو لوزی و اندازهٔ ضلع لوزی کوچک خواهیم داشت:

$\frac{2}{5} = \frac{6}{y} \Rightarrow y = 15$ اندازهٔ ضلع لوزی بزرگ

محیط لوزی بزرگ: $15 \times 4 = 60 \Rightarrow $ محیط تقسیم بر مساحت $\frac{{60}}{{100\sqrt 5 }} = \frac{3}{{5\sqrt 5 }} = \frac{{3\sqrt 5 }}{{25}}$