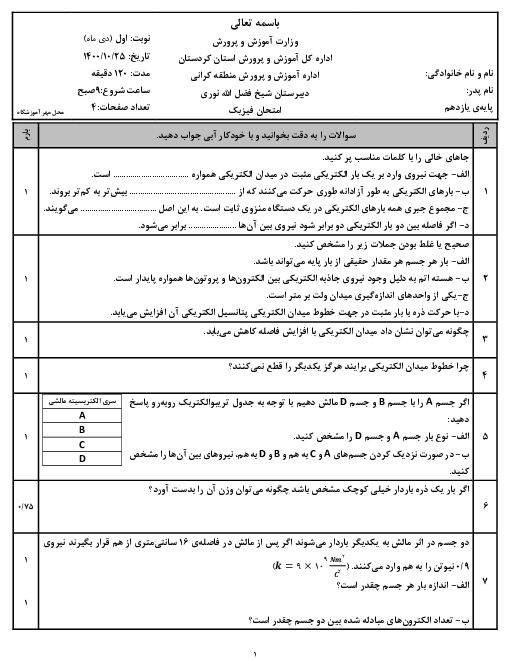
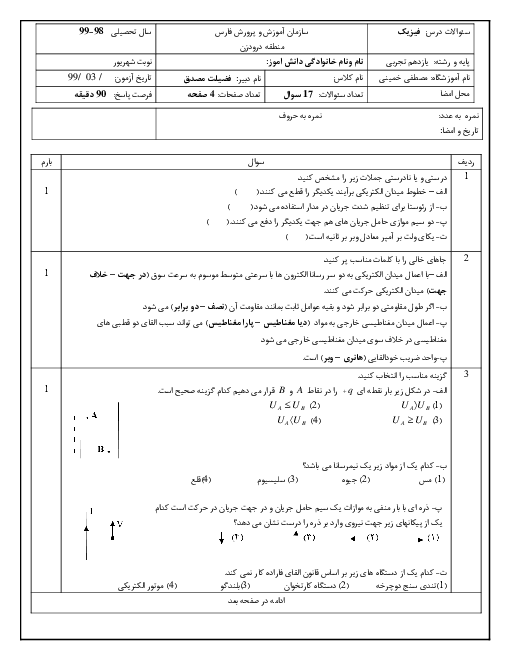
در حالت اول نیروی خالص وارد بار $-q$ در نقطهٔ B به صورت زیر است:
به تصویر شماره 1 توجه شود.

${{F}_{AB}}={{F}_{CB}}=\frac{k\left| q \right|\left| -q \right|}{{{(\sqrt{2}r)}^{2}}}=\frac{k{{q}^{2}}}{2{{r}^{2}}}$
${{\overrightarrow{F}}_{CB}},{{\overrightarrow{F}}_{AB}}$ برایند دو نیروی: ${{F}_{R}}=\sqrt{F_{AB}^{2}+F_{CB}^{2}}=\sqrt{2}{{F}_{AB}}=\sqrt{2}\frac{k{{q}^{2}}}{2{{r}^{2}}}$
${{F}_{OB}}=\frac{k\left| -q \right|\left| -q \right|}{{{r}^{2}}}=\frac{k{{q}^{2}}}{{{r}^{2}}}$
${{F}_{T,B}}={{F}_{OB}}-{{F}_{R}}=\frac{k{{q}^{2}}}{{{r}^{2}}}-\frac{\sqrt{2}}{2}\frac{k{{q}^{2}}}{{{r}^{2}}}=(1-\frac{\sqrt{2}}{2})\frac{k{{q}^{2}}}{{{r}^{2}}}=0/3\frac{k{{q}^{2}}}{{{r}^{2}}}$

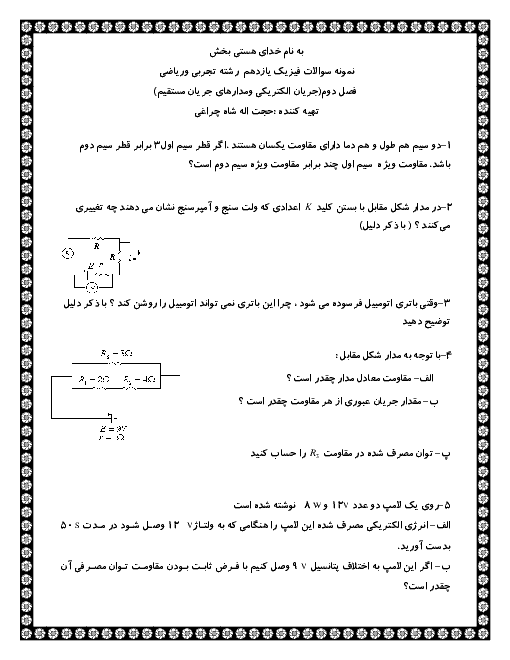
در حالت دوم داریم:
توجه شود به تصویر 2

${{F}_{AB}}={{F}_{CB}}=\frac{k{{q}^{2}}}{2{{r}^{2}}}$
${{F}_{OB}}=\frac{k{{q}^{2}}}{{{r}^{2}}}$
$\overrightarrow{{{{{F}'}}_{R}}}=\sqrt{F_{AB}^{2}+F_{CB}^{2}}=\sqrt{2}{{F}_{AB}}=\frac{\sqrt{2}}{2}\frac{k{{q}^{2}}}{{{r}^{2}}}$
${{{F}'}_{T,B}}=\sqrt{F_{OB}^{2}+F_{R}^{2}}=\sqrt{{{(\frac{k{{q}^{2}}}{{{r}^{2}}})}^{2}}+{{(\frac{\sqrt{2}}{2}\frac{k{{q}^{2}}}{{{r}^{2}}})}^{2}}}=\sqrt{\frac{3}{2}}\frac{k{{q}^{2}}}{{{r}^{2}}}\simeq 1/2\frac{k{{q}^{2}}}{{{r}^{2}}}\Rightarrow {{{F}'}_{T,B}}>{{F}_{T,B}}$

یعنی نیروی برایند افزایش می‌یابد.