نمودار مکان ـ زمان متحرکی که روی خط راست حرکت می‌کند، به‌صورت شکل زیر است. اگر این متحرک در لحظۀ در فاصلۀ 8 متری از مکان اولیۀ خود و در لحظۀ که در خلاف جهت محور… | فیزیک (3) تجربی دوازدهم شماره 221042

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 1: حرکت بر خط راست فیزیک (3) تجربی دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

نمودار مکان ـ زمان متحرکی که روی خط راست حرکت می‌کند، به‌صورت شکل زیر است. اگر این متحرک در لحظۀ ${{t}_{1}}$ در فاصلۀ 8 متری از مکان اولیۀ خود و در لحظۀ ${{t}_{2}}$ که در خلاف جهت محور x در حال حرکت است، در فاصلۀ 8 متری از بیش‌ترین فاصلۀ خود از مبدأ مکان قرار داشته باشد، ${{t}_{1}}$ و ${{t}_{2}}$ به‌ترتیب از راست به چپ برحسب ثانیه کدام‌اند؟

1 )

1 و 7

2 )

2 و 7

3 )

2 و 10

4 )

1 و 10

نمایش پاسخ

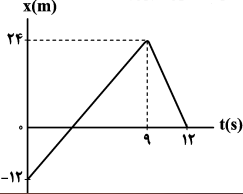
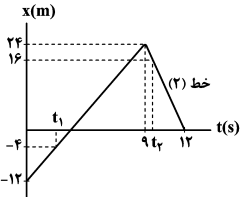
مکان اولیۀ این متحرک (در t = 0) برابر با ${{x}_{0}}=-12m$ است. پس زمانی که متحرک در فاصلۀ 8 متری از مکان اولیۀ خود قرار دارد، در واقع در مکان ${{x}_{1}}=-4m$ قرار خواهد داشت. با توجه به تشابه مثلث‌ها داریم:

$ \frac{24-(-12)}{9}=\frac{-4-(-12)}{{{t}_{1}}} \Rightarrow {{t}_{1}}=2s$

از طرفی طبق نمودار، بیش‌ترین فاصلۀ متحرک از مبدأ مکان برابر 24m است که در t = 9s رخ داده است. هم در زمان‌های قبل از t = 9s و هم در زمان‌های بعد از t = 9s ، متحرک می‌تواند در 8 متری از این نقطه قرار گیرد، اما با توجه به اینکه طبق اطلاعات سؤال در لحظۀ ${{t}_{2}}$ متحرک در حال حرکت در خلاف جهت محور x بوده است، پس لحظۀ ${{t}_{2}}$ پس از t = 9s و مکان متحرک در این لحظه x = 24 - 8 = 16m بوده است. در این حالت نیز با توجه به تشابه مثلث‌ها داریم:

$\frac{24-0}{12-9}=\frac{16-0}{12-{{t}_{2}}}\Rightarrow {{t}_{2}}=10s$