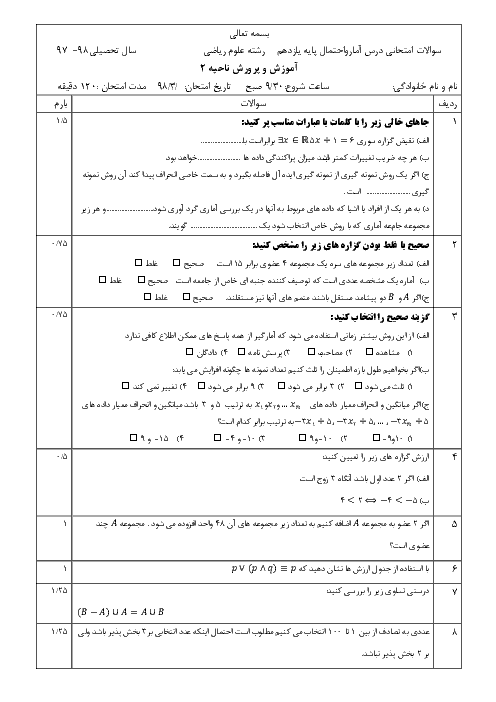
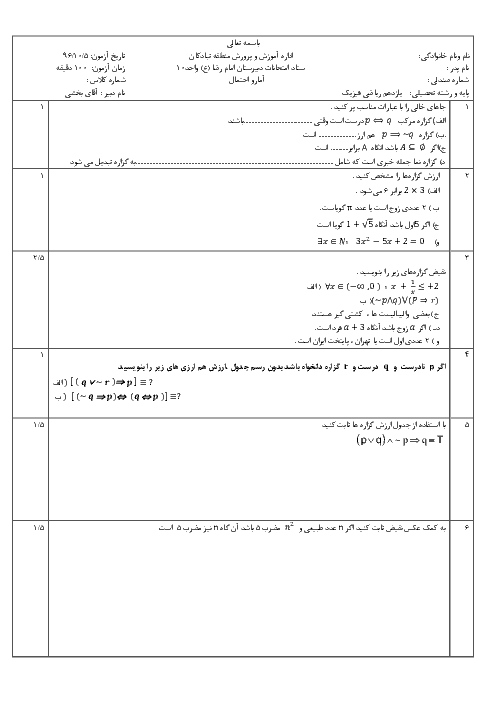
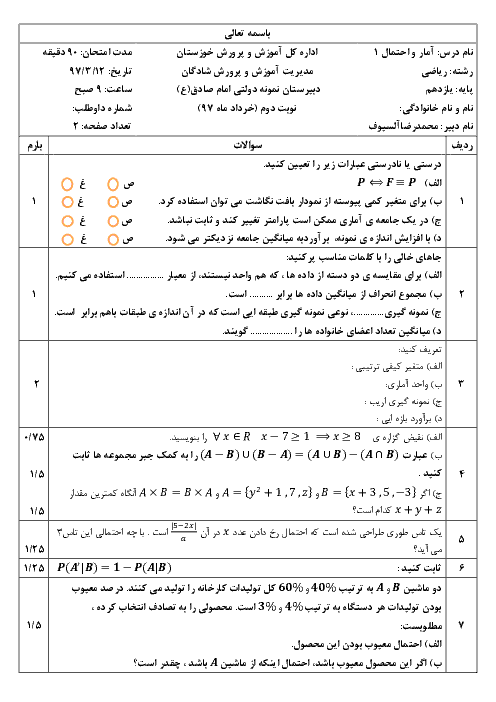
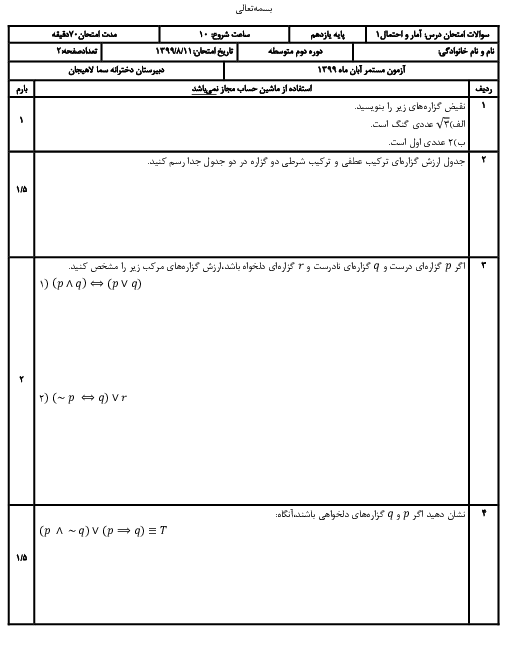
نكته‌ی 1: نمودار جعبه‌ای نموداری است كه پراكندگی داده‌ها را بر اساس پنج معيار  1) كوچك‌ترين داده  2) چارك اول  3) ميانه  4) چارك سوم  5) بزرگ‌ترين داده به‌صورت زیر نمايش می‌دهد.

نكته‌ی 2: در داده‌های مرتب‌شده به‌صورت صعودی:

الف) اگر تعداد داده‌ها فرد باشد، داده‌ی وسط، ميانه است.

ب) اگر تعداد داده‌ها زوج باشد، ميانگين دو داده‌ی وسط، ميانه است.

ج) ميانه‌ی نيمه‌ی اول داده‌ها را با ${{Q}_{1}}$ نمایش داده و چارک اول می‌نامیم.

د) ميانه‌ی نيمه‌ی اول داده‌ها را با ${{Q}_{3}}$ نمایش داده و چارک سوم می‌نامیم.

نکته‌ی 3: واریانس داده‌های آماری ${{x}_{1}}$، ${{x}_{2}}$، ${{x}_{3}}$، ... و ${{x}_{n}}$ را با $\sigma _{n}^{2}$ نمایش داده و برابر است با:

${{\sigma }^{2}}=\frac{\sum\limits_{i=1}^{n}{{{({{x}_{i}}-\overline{x})}^{2}}}}{n}$

نکته‌ی 4: ضریب تغییرات داده‌های ${{x}_{1}}$، ${{x}_{2}}$، ${{x}_{3}}$، ... و ${{x}_{n}}$ برابر است با خارج‌قسمت تقسیم انحراف‌معیار داده‌ها $(\sigma )$ بر میانگین داده‌ها $(\overline{x})$ که آن‌را با CV نمایش می‌دهیم:

$CV=\frac{\sigma }{\overline{x}}$

نکته‌ی 5: انحراف‌معیار برابر است با جذر واریانس: $\sigma =\sqrt{{{\sigma }^{2}}}$

نکته‌ی 6: مشاهده‌ای كه تفاوت بسيار زيادی با ساير مشاهدات داشته باشد را داده‌ی دورافتاده می‌گوييم.

ابتدا داده‌ها را مرتب شده می‌نویسیم، با توجه به نکات 1 و 2 داریم:

$\overbrace{3,4,\underset{\underset{{{Q}_{1}}}{\mathop{\downarrow }}\,}{\mathop{6}}\,,7,8}^{Nimeaye\,Aval},\underset{Mianeh}{\mathop{\underset{\downarrow }{\mathop{9}}\,}}\,,\overbrace{10,11,\underset{\underset{{{Q}_{3}}}{\mathop{\downarrow }}\,}{\mathop{12}}\,,40,60}^{Nimeaye\,Dovom}$

داده‌های داخل جعبه در این حالت عبارتند از: $7,8,9,10,11$ پس با توجه به نکات 3، 4 و 5 داریم:

$\begin{align}
  & \overline{x}=\frac{45}{5}=9 \\ 
 & \sigma =\sqrt{\frac{{{(9-7)}^{2}}+{{(9-8)}^{2}}+{{(9-9)}^{2}}+{{(9-10)}^{2}}+{{(9-11)}^{2}}+}{5}}=\sqrt{2} \\ 
 & CV=\frac{\sigma }{\overline{x}}=\frac{\sqrt{2}}{9}\,\,\,\,\,(1) \\ 
\end{align}$

اینک با توجه به نکته‌ی 6، دو داده‌ی 40 و 60 كه داده‌ی دورافتاده هستند را حذف كرده و به‌كمك نكات 1، 2 و 3 واریانس داده‌های داخل جعبه را حساب می‌کنیم:

$\overbrace{3,\underbrace{4,6}_{\underset{{{Q}_{1}}=5}{\mathop{\downarrow }}\,},7,}^{Nimeaye\,Aval}\underset{Mianeh}{\mathop{\underset{\downarrow }{\mathop{8}}\,}}\,,\overbrace{9,\underbrace{10,11}_{\underset{{{Q}_{1}}=10/5}{\mathop{\downarrow }}\,},12}^{Nimeaye\,Dovom}$

داده‌های داخل جعبه در این حالت، عبارتند: $6,7,8,9,10$

$\begin{align}
  & \bar{x}=\frac{40}{5}=8 \\ 
 & {{\sigma }^{2}}=\frac{{{(6-8)}^{2}}+{{(7-8)}^{2}}+{{(8-8)}^{2}}+{{(9-8)}^{2}}+{{(10-8)}^{2}}}{5}=\frac{10}{5}=2(2) \\ 
\end{align}$

و در نهایت خواهیم داشت:

$\frac{(2)}{(1)}=\frac{2}{\frac{\sqrt{2}}{9}}=\frac{18}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}=\frac{18\sqrt{2}}{2}=9\sqrt{2}$