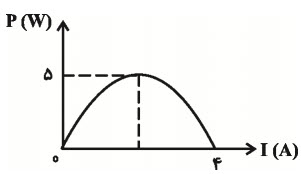
شكل زير، نمودار توان خروجی يک مولد را برحسب جريان عبوری از آن نشان می‌دهد. نيروی محركه و مقاومت درونی مولد به ترتيب از راست به چپ برحسب واحدهای $SI$ كدام است؟