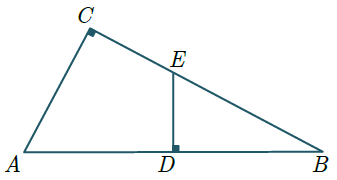
$AC = 12$

$AD = BD = 10$

${S_{ACED}} = {S_{ABC}} - {S_{EDB}}$

قائم الزاویه $ \Rightarrow BC = \sqrt {A{B^2} - A{C^2}}  = \sqrt {400 - 144}  = \sqrt {265}  = 16$

$\mathop {ABC}\limits^\Delta   \to $

اما

$\begin{array}{*{20}{c}}
  {\mathop {ACB}\limits^ \wedge   = \mathop {EDB}\limits^ \wedge  } \\ 
  {\mathop {ABC}\limits^ \wedge   = \mathop {DBE}\limits^ \wedge  } \\ 
  {\mathop {CAB}\limits^ \wedge   = \mathop {DEB}\limits^ \wedge  } 
\end{array} \Rightarrow \mathop {ABC}\limits^ \wedge   \sim \mathop {DEB}\limits^ \wedge   \Rightarrow \frac{{AB}}{{EB}} = \frac{{AC}}{{DE}} = \frac{{BC}}{{DB}} \Rightarrow \frac{{20}}{{EB}} = \frac{{12}}{{DE}} = \frac{{16}}{{10}} = \frac{8}{5}$

پس نسبت تشابه $\frac{8}{5}$ است. می‌توان اضلاع مثلث $\mathop {ABD}\limits^\Delta  $ را یافت و سپس مساحت را محاسبه و جواب را یافت:

$\frac{{{S_{ABC}}}}{{{S_{EBD}}}} = \frac{{64}}{{25}} \to {S_{EBD}} = \frac{{25}}{{64}}{S_{ABC}}$

$\begin{gathered}
  {S_{ABC}} = \frac{{16 \times 12}}{2} = 96 \hfill \\
   \Rightarrow {S_{ACED}} = {S_{ABC}} - \frac{{25}}{{64}}{S_{ABC}} = \frac{{39}}{{64}}{S_{ABC}} \to \frac{{39}}{{\mathop {\cancel{{64}}}\limits_{\mathop {\cancel{8}}\limits_2 } }} \times \mathop {\cancel{{96}}}\limits^{\mathop {\cancel{{12}}}\limits^3 }  = \frac{{117}}{2} = 58/5 \hfill \\ 
\end{gathered} $