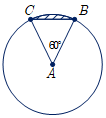
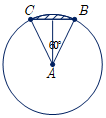
از آنجاکه AB و AC باهم برابرند و زاویهٔ A برابر 60 درجه است می‌توان نتیجه گرفت که مثلث ABC یک مثلث متساوی‌الاضلاع است و AH هم ارتفاع و هم میانه است. از طرفی $\hat A = {60^ \circ }$، بنابراین مساحت این قسمت از دایره $\frac{1}{6}$ مساحت کل دایره خواهد بود.

با توجه به رابطهٔ فیثاغورس داریم:

$\mathop {ABC}\limits^\Delta  :A{H^2} = A{B^2} - B{H^2}$

$\xrightarrow{{AB = AC = BC = 2\sqrt {\sqrt 3 } \pi }}A{H^2} = {(2\sqrt {\sqrt 3 } \pi )^2} - {(\sqrt {\sqrt 3 } \pi )^2}$

$ = 4\sqrt 3 {\pi ^2} - \sqrt 3 {\pi ^2} = 3\sqrt 3 {\pi ^2} \Rightarrow AH = \sqrt {3\sqrt 3 } \pi $

حالا می‌توانیم مساحت مثلث و $\frac{1}{6}$ دایره را یافته و از هم کم کنیم تا مساحت قسمت رنگی حاصل شود.

${S_{\mathop {ABC}\limits^\Delta  }} = \frac{{AH \times BC}}{2} = \frac{{\sqrt {3\sqrt 3 } \pi  \times \cancel{2}\sqrt {\sqrt 3 } \pi }}{{\cancel{2}}} = 3{\pi ^2}$

مساحت یک ششم دایره: $\frac{1}{6} \times (2\sqrt {\sqrt 3 } \pi )(2\sqrt {\sqrt 3 } \pi )\pi  = \frac{4}{6}\sqrt 3 {\pi ^2} = \frac{2}{3}\sqrt 3 {\pi ^2}$

مساحت قسمت رنگی: $\frac{2}{3}\sqrt 3 {\pi ^2} - 3{\pi ^2} = {\pi ^2}(\frac{2}{3}\sqrt 3 \pi  - 3)$