ابتدا ضابطهٔ تابع را ساده‌تر كنيم:

$y=a\sin \pi (\frac{1}{2}-bx)+c\Rightarrow y=a\sin (\frac{\pi }{2}-b\pi x)+c\Rightarrow y=a \cos b\pi x+c$

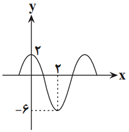
فاصلهٔ افقی بين مينيمم و ماكزيمم متوالی برابر $\frac{T}{2}$ است پس داريم: 

$\frac{T}{2}=2\Rightarrow T=4\Rightarrow \frac{2\pi }{\left| x \right|}=4\Rightarrow \frac{2\pi }{\left| bx \right|}=4\Rightarrow \left| b \right|=\frac{1}{2}\Rightarrow b=\pm \frac{1}{2}$

هر دوی $\pm \frac{1}{2}$ قابل‌قبول است، زيرا $\cos (-x)=\cos x$. مطابق شكل ماكزيمم تابع 2 و مينيمم تابع 6- است. پس:

$\left\{ \begin{matrix} \left| a \right|=\frac{\max -\min }{2}=\frac{2-(-6)}{2}=\frac{8}{2}=4\Rightarrow a=\pm 4 \\ c=\frac{\max +\min }{2}=\frac{2+(-6)}{2}=\frac{-4}{2}=-2  \\ \end{matrix} \right.$

شكل داده شده، فرمت تابع $\cos x$ را دارد. پس فقط $a=4$ صحيح است و داريم:

$f(x)=4\cos \frac{\pi }{2}x-2$

$\xrightarrow{x=\frac{7}{3}}f(\frac{7}{3})=4\cos (\frac{\pi }{2}\times \frac{7}{3})-2=4\cos \frac{7\pi }{6}-2$

$\Rightarrow f(\frac{7}{3})=4\cos (\pi +\frac{\pi }{6})-2=4(-\cos \frac{\pi }{6})-2=-4\times \frac{\sqrt{3}}{2}-2=-2\sqrt{3}-2$