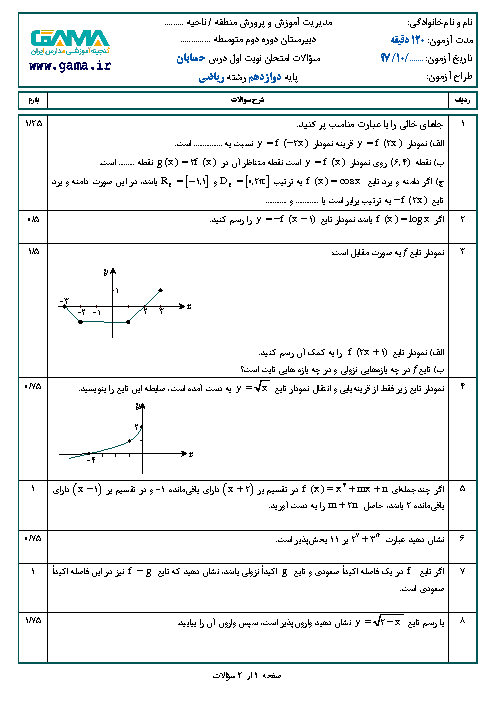
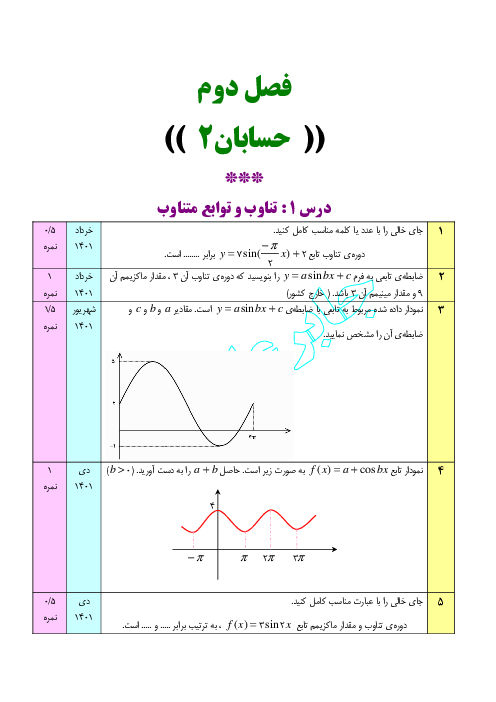
درس 1: اکسترممهای یک تابع و توابع صعودی و نزولی
حسابان (2)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
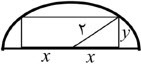
یک مستطیل در یک نیمدایره محاط شده است. اگر شعاع دایره 2 سانتیمتر باشد، طول و عرض مستطیل را طوری به دست آورید که مساحت آن بیشترین مقدار ممکن باشد.
پاسخ تشریحی :