درس 3: اعمال بر روی توابع
ریاضی و آمار (2)
یازدهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
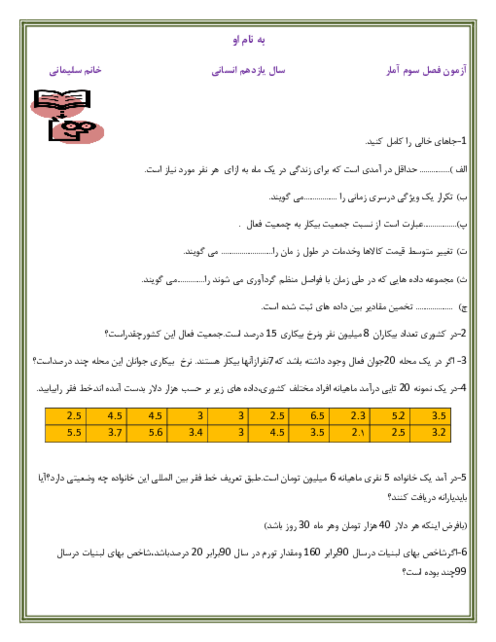
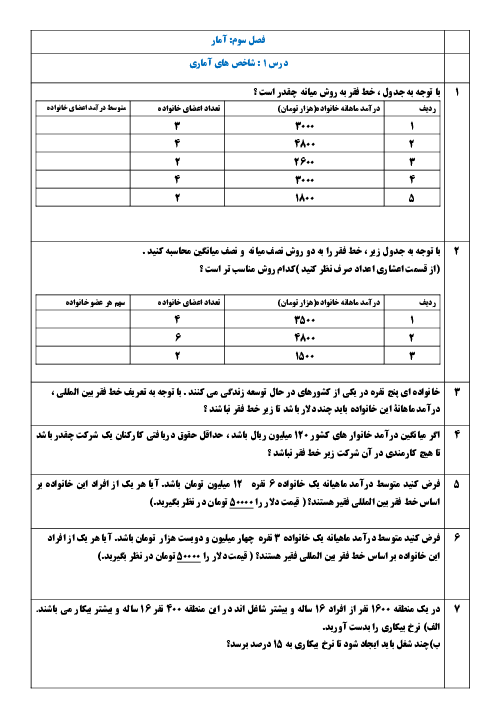
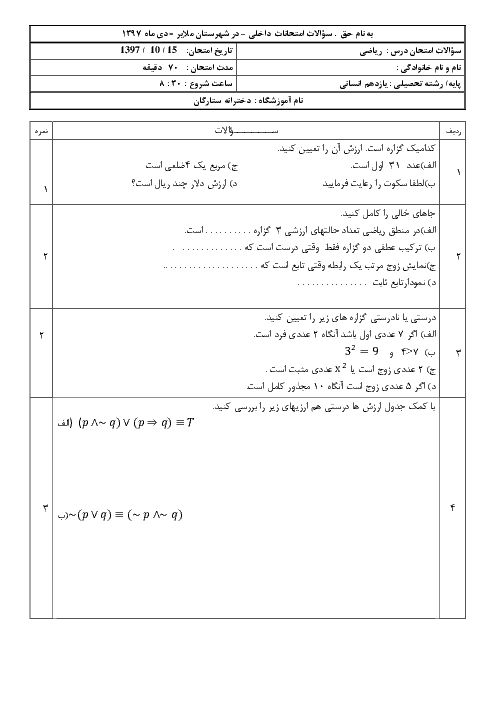
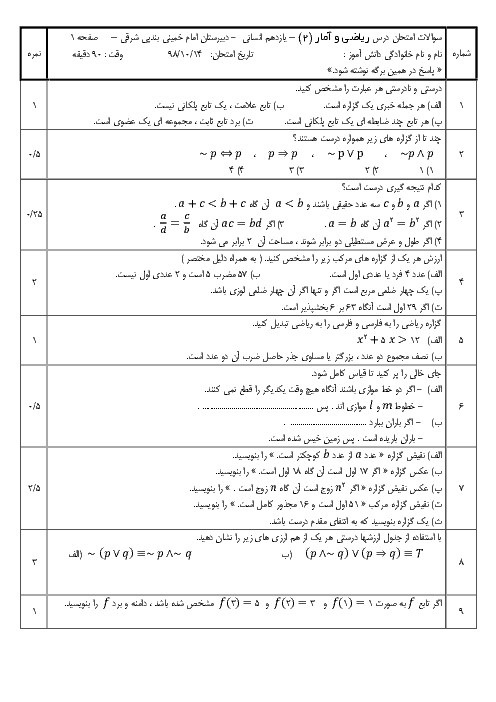
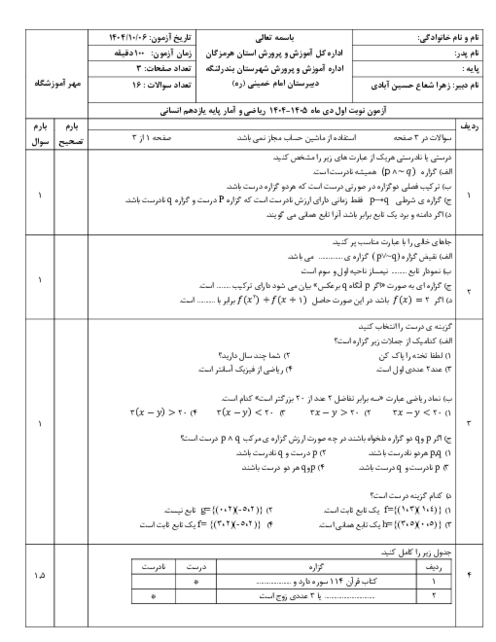
اگر تابع $f=\left\{ (2,5),(3,0),(4,1),(-1,1) \right\}$ و تابع $\frac{f}{g}=\left\{ (3,0),(4,\frac{1}{5}) \right\}$ باشد، تابع $g$ كداميک از موارد زير میتواند باشد؟
1 )
$g=\left\{ (1,1),(3,2),(5,5),(-1,0) \right\}$
2 )
$g=\left\{ (2,1),(3,1),(1,-1),(4,5) \right\}$
$g=\left\{ (-1,0),(3,3),(1,2),(4,5) \right\}$
4 )
$g=\left\{ (-2,2),(3,-3),(4,1),(1,0) \right\}$
پاسخ تشریحی :
تحلیل ویدئویی تست
شبنم غلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...