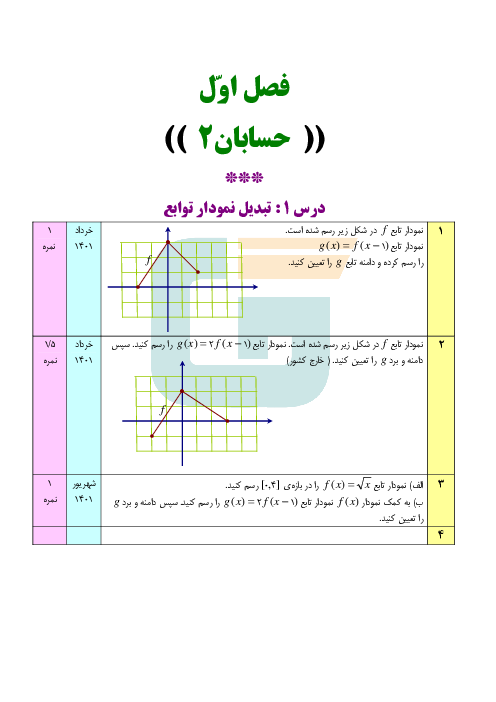
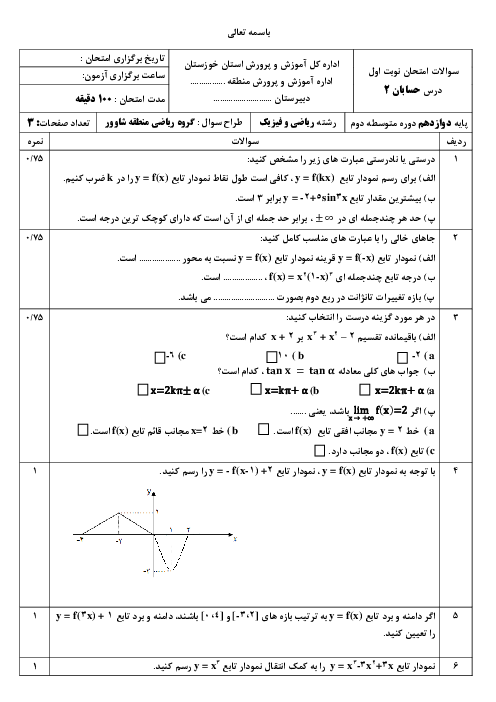
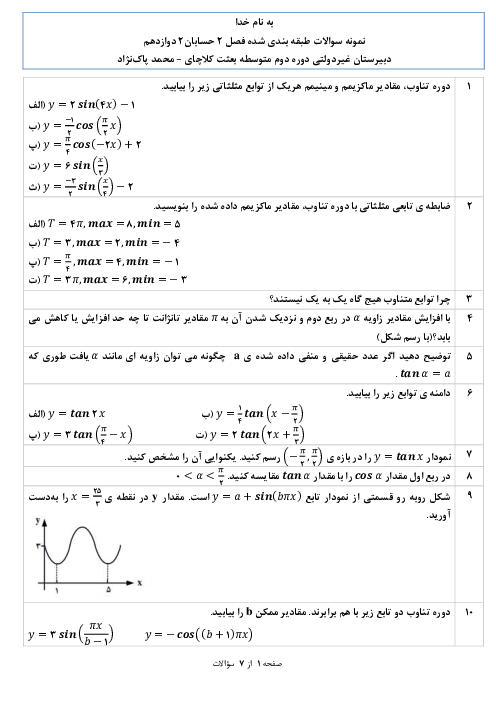
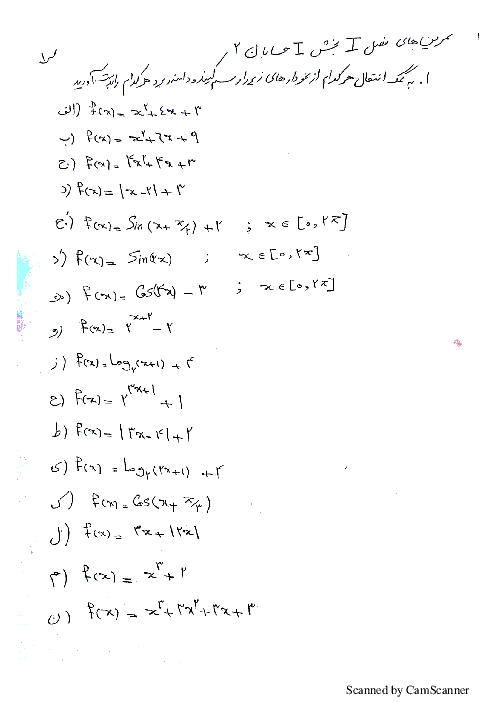$\underset{x\to -1}{\mathop{\lim }}\,\frac{x+2}{-4{{(x+1)}^{2}}}=-\infty \Rightarrow -4{{x}^{2}}+ax+b=- {{(x+1)}^{2}}$
$\Rightarrow -4{{x}^{2}}+ax+b=-4{{x}^{2}}-8x- \xrightarrow{Moghayeseyeh\,\,Nazir\,Be\,Nazir}\left\{ \begin{matrix} a=-8 \\ b=-4 \\ \end{matrix} \right.$
$\underset{x\to 1}{\mathop{\lim }}\,\frac{\tan \pi x}{a{{x}^{2}}-2b}=\underset{x\to 1}{\mathop{\lim }}\,\frac{\tan \pi x}{-8{{x}^{2}}+8}\underset{x\to 1}{\mathop{\lim }}\,\frac{-\tan (\pi -\pi x)}{-8(x- )(x+1)}$
$=\frac{1}{8}\underset{x\to 1}{\mathop{\lim }}\,\left( \frac{\tan (-\pi (x-1))}{x-1} \right)\left( \frac{1}{x+1} \right)=-\frac{\pi }{8}(\frac{1}{2})=-\frac{\pi }{16}$