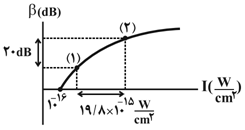
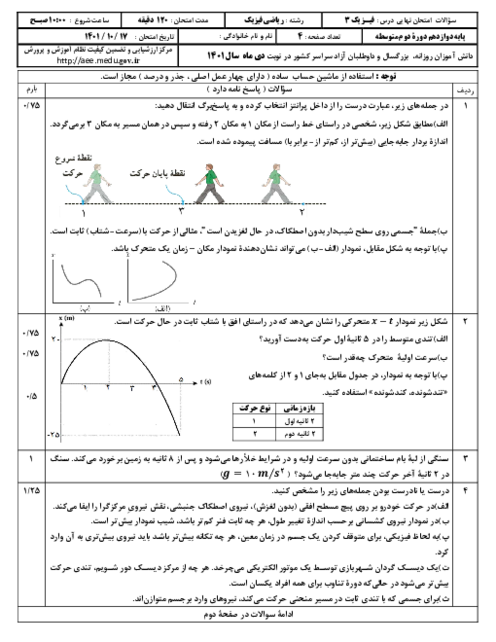با توجه به اطلاعات روی نمودار می‌توان نوشت:

$\left\{ \begin{matrix} {{\beta }_{2}}-{{\beta }_{1}}=20dB  \\ {{I}_{2}}-{{I}_{1}}=19/8\times {{10}^{-15}}\frac{W}{c{{m}^{2}}}  \\ \end{matrix} \right.$

$\Delta \beta =10\log \frac{{{I}_{2}}}{{{I}_{1}}}\Rightarrow 20=10\log \frac{{{I}_{2}}}{{{I}_{1}}}\Rightarrow \frac{{{I}_{2}}}{{{I}_{1}}}={{10}^{2}}\Rightarrow {{I}_{2}}={{10}^{2}}{{I}_{1}}$

${{I}_{2}}-{{I}_{1}}=19/8\times {{10}^{-15}}\Rightarrow {{10}^{2}}{{I}_{1}}-{{I}_{1}}=19/8\times {{10}^{-15}}$

$\Rightarrow 99{{I}_{1}}=19/8\times {{10}^{-15}}\Rightarrow {{I}_{1}}=2\times {{10}^{-16}}\frac{W}{c{{m}^{2}}}=2\times {{10}^{-12}}\frac{W}{{{m}^{2}}}$

${{I}_{1}}=\frac{\overline{P}}{{{A}_{1}}}=\frac{\overline{P}}{4\pi r_{1}^{2}}\Rightarrow 2\times {{10}^{-12}}=\frac{2/4\times {{10}^{-13}}}{4\times 3\times r_{1}^{2}}\Rightarrow r_{1}^{2}=0/01\Rightarrow {{r}_{1}}=0/1m=10cm$