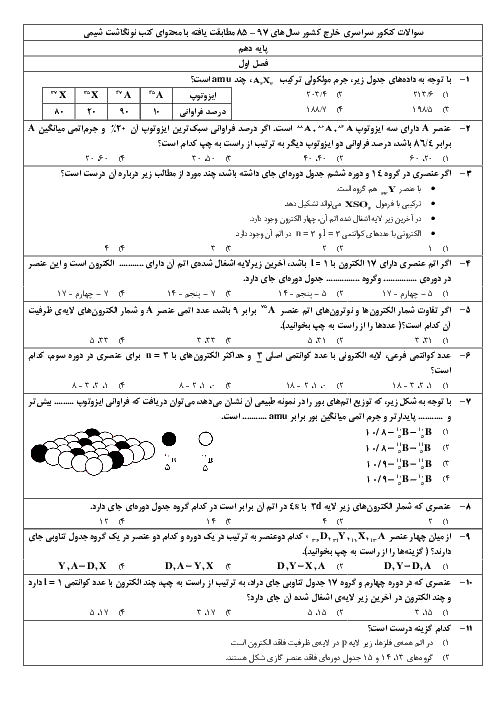
در 250 میلی‌لیتر از محلول باز قوی MOH در دمای اتاق، $2/5 \times {10^{ - 10}}$ مول یون ${H_3}{O^ + }(aq)$ وجود دارد، محلول این باز، چند مولار است و غلظت یون $O{H^ - }$ در آن با غلظت این یون در محلول چند مولار باریم هیدروکسید برابر است؟
1 )
$2/5 \times {10^{ - 10}},1 \times {10^{ - 9}}$
2 )
$5 \times {10^{ - 10}},1 \times {10^{ - 9}}$
3 )
$2 \times {10^{ - 6}},1 \times {10^{ - 5}}$
$5 \times {10^{ - 6}},1 \times {10^{ - 5}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...