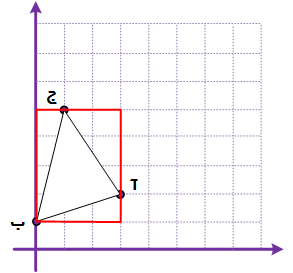
اگر نقاط $\left[ \begin{matrix} 3 \\ 2 \\ \end{matrix} \right]$ =آ، $\left[ \begin{matrix} 0 \\ 1 \\ \end{matrix} \right]$ =ب و $\left[ \begin{matrix} 1 \\ 5 \\ \end{matrix} \right]$ =ج مختصات رأسهای یک مثلث باشند، مساحت قرینهی مثلث (آ ب ج) نسبت به مرکز تقارن $\left[ \begin{matrix} 5 \\ 3 \\ \end{matrix} \right]$ کدام است؟
تحلیل ویدئویی تست
ریحانه احمدی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...